輕鬆談演算法的複雜度分界：什麼是P, NP, NP-Complete, NP-Hard問題

在寫程式的時候，會聽到有人說這些問題是NP-Complete問題，或說這些是P問題，那這到底是什麼東西？其實這就是一套定義演算法複雜度的方法，今天我就想帶大家來聊聊這個艱澀但有趣的話題。

Turing Machine

我們先從 Turing machine（圖靈機）開始講起，Turing machine是現代電腦的基本雛型，是英國數學家圖靈（Alan Turing）於1936年提出的一種抽象計算模型，這個計算模型在猜想上可以「計算所有在演算法中可計算的問題」，也就是可以解決人類所有可解的問題，這個猜想稱之為 Church–Turing thesis（thesis代表假設或猜想），僅管目前還無法證明這個猜想，但是目前為止它幾乎是完全被接受的。

簡單的談一下 Turing machine的基本架構，首先我們需要一個磁帶，這一條磁帶上面可以一格一格的填入一些 symbols，這可以是單純的 0/1 symbols 或者更多種類的 symbols，但這些 symbols 的數量必須是有限的，而這個symbols就可以當作我的輸入，接下來我需要一個讀寫頭，這個讀寫頭會在磁帶上讀取或寫入 symbol，或左右移動，另外這個讀寫頭存有一個 state，這個 state 會隨著狀況改變，然後我就利用 symbol 和 state 來建立一個規則表，舉個例子，譬如說：初始的 state 是 \(q_0\)，如果讀寫頭在 \(q_0\) 的情況下讀到 symbol 0，就寫入 symbol 1，並且向右移動3格，並且改變 state \(q_0\) 為 \(q_1\)，... 等等，藉由可操作的規則來完成我們想做的運算，最後最重要的是它必須有一個 halt state 讓機器知道已經計算完畢了。Turing machine 不僅僅在理論上可以做任何的計算，而更有價值的是 Turing machine 的架構是有辦法用物理的方式來製造的，所以才會有現代電腦這玩意兒。

說到電腦，更嚴謹地說，我們當今的電腦架構是比較接近 deterministic Turing machine (DTM)，與之對比的是 non-deterministic Turing machine (NTM)，我來好好的解釋一下，deterministic 的中文稱為決定性，所以 non-deterministic 就是非決定性。

如果給予 Turing machine 某個 state 和某個 symbol 下，它的下一步如果只有一種可能，那我們就稱它為 deterministic Turing machine (DTM)，

所以上述的讀取頭每次就依照當下特定的 symbol 和 state 然後「決定」下一步應該要怎麼動作。

但是 non-deterministic Turing machine (NTM) 就不拘於此，針對某個 state 和某個 symbol 它的下一步可能會有很多種，它會是一個分支，它可能同時要向右移3格，又同時要向左移動2格，所以你可以想像一下你的讀寫頭一分為二，然後再各自進行自己的任務，這個分支可以有無限多個，只要最後有某個分支到達 halt state，我們就解完問題並停止計算，這就是 non-deterministic Turing machine (NTM)。

顯而易見的，DTM 只是 NTM 的特例，所以 NTM 比 DTM 擁有更快的計算速度，但這裡不要誤會喔！不管是 DTM 和 NTM 能解的問題是一樣多的，而且在數學上可以將 NTM 的計算方式轉換成 DTM 的計算方式，他們差異點只是解決相同問題所用到的時間複雜度不一樣，不過這就很關鍵。

時間複雜度

接下來，我要開始切入正題，我們來聊聊時間複雜度吧！什麼是時間複雜度呢？時間複雜度用來評估演算法需要花多少時間做計算，我們常用大O符號來描述，代表的是一個漸進的函數數量級上界，舉個例子，假設我想要在一個有序的數列\(2,3,5,7,13,27\)中找到\(7\)的位置，最簡單的做法就是從第一個元素開始檢查起，如果不是元素\(7\)就再找下一個，直到找到為止，所以最差的情形就是我一路找直到了最後一個元素，如果數列有\(Ｎ\)個元素，我們最差的情形就是做了\(Ｎ\)次的比較，而每次做比較所花的時間是一個常數時間，因此這個演算法的上界將被 \(a×N\) 所界定，\(a\)為常數，所以這個演算法的時間複雜度為\(O(N)\)，再舉個稍微難一點的例子：子集合加總問題，假設給予一組集合\(\{−7, −3, −2, 5, 8\}\)，然後問是否有一組子集合相加為\(0\)，怎麼做呢？最簡單的做法就是，窮舉出所有可能的子集合然後相加驗證是否剛好為0，假設集合中有Ｎ個元素，我會有\(2^N\)種的子集合，而且要加總最多\(Ｎ\)個元素，所以這個過程的時間複雜度為 \(O(N×(2^N))\)。特別提醒，以上的分析方式大致上是符合DTM和現代電腦的運作方式，一步接著一步做（step-by-step），而NTM就不這麼分析問題，當然兩者看待同一個問題的時間複雜度就會不一樣。

剛剛有提到 Turing machine 可以解所有演算法問題，那如果我製造一台機器符合 Turing machine或者是我購買一台電腦，是不是就可以躺著解所有的問題了，很可惜的，並不是的！我們剛剛有簡單的帶大家了解時間複雜度，我們知道每種演算法有其計算時間，子集合加總問題的時間複雜度為\(O(N×(2^N))\)，如果今天很單純的，我的元素只有\(1000\)個，這個數量不過分吧！但大家試著計算一下\(1000 ×(2^{1000})\)就會發現這是一個天文數字，它大到縱使每個計算只需要\(0.00001\)秒，也需要遠遠超過地球年齡的時間才有辦法算完，因此這類問題就算是可解的，也並不實際代表你可以解完，因為你必須考慮解問題要花多少時間。

所以現實面是只有在一個數量級時間以下的問題我們才好應付，這個數量級被稱為 polynomial time（多項式時間），用大\(Ｏ\)表示為\(Ｏ(N^k)\)，剛剛上面提到的數列找元素問題，它得時間複雜度為\(O(N)\)，為 polynomial time，這是屬於好對付的問題，如果超過 polynomial time 的問題我們稱為 intractable problem (難解的問題)。

P＝NP？

如果有一群演算法用DTM來做計算所需時間是 polynomial time，那這類演算法或問題被稱為Ｐ問題，Ｐ就是 polynomial-time 的縮寫。

另外如果有一群演算法用NTM來做計算所需時間是 polynomial time，那這類問題被稱為NP問題，NP是 non-deterministic polynomial-time 的縮寫。

NP問題還有另一個數學上等價的判斷方法，從驗證解的難度來界定，如果用DTM來驗證一組解是否正確只需要 polynomial time，那這個問題就是一個NP問題，剛剛子集合加總問題，我們要驗證解是否正確很簡單也很快速，我們只要把解的數字加總起來看是不是為\(0\)就可以了，所以子集合加總問題是一個NP問題，但因為這個問題的時間複雜度為 \(O(N×(2^N))\)，所以它不是一個Ｐ問題。

如果有一天我們可以找到一種演算法來解所有的NP問題，並且只需要 polynomial time，那這些問題就是既是NP問題也是P問題了，也就是代表今天你用DTM和NTM都可以在polynomial time以內把問題解完，有這麼好的事嗎？這就牽扯出一樁數學懸案。

在討論這個問題之前，我先補充一件事，剛剛我提到NP問題有兩種定義是等價的，

Definition of NP problem:

NTM可在 polynomial time 內解決的問題 \(\equiv\) 問題的解有辦法在DTM polynomial time下被驗證

這兩種定義如何連結起來呢？我來粗略地說明一下，因為NTM有無窮多個分支讓我利用，那我就讓每個分支去窮舉每種可能的解，然後再驗證每個分支的解是否正確，而驗證的過程只需要 polynomial time，所以自然在NTM下我只需要 polynomial time 就可以將這個問題給解完，也因此它們是等價的。

那也許大家還有一個疑問，有什麼問題是無法在 polynomial time 內驗證解的？我們稍稍的改一下子集合加總問題，改問「這集合之中最多有多少種子集合符合加總為\(0\) ?」這時候如果我告訴你解是\(3\)個，你要怎麼驗證這個答案是對的，你會發現你幾乎還是需要再重新解同樣的問題才有辦法驗證，這種問題被稱為Co-NP問題（反NP問題）。

毋庸置疑的，NP問題必定包含P問題，在DTM之下為 polynomial time 可解決的，在NTM之下也必定是 polynomial time 可解決的，但是P問題會等價於NP問題嗎？（P=NP?）這個問題到目前為止還是數學界無法證明的問題，目前既不能證明\(P=NP\)也不能證明\(P\neq NP\)，克雷數學研究所曾在2000年公布千禧年大獎七大難題，每解破一題的解答者，會頒發獎金100萬美元，裡面的其中一題就是\(P=NP\)?問題，那為什麼這個問題很重要呢？ 舉個例子，有一種我們現今常用的加密方法叫做RSA加密，它的概念非常的簡單，RSA加密利用兩個大質數相乘的合數當作驗證，只有用這兩個大質數的其中一個才有辦法整除它並解鎖，如果你想要暴力破解這個鎖是很困難的，你需要超過 polynomial time 的時間，但是你要驗證解是否正確是很容易的，根據剛剛的論述，RSA加密是一個NP問題，如果今天有人找到方式可以把NP問題當作P問題處理，也就是說他可以輕易地用現代的電腦去解開RSA加密，不僅如此，目前的加密方法幾乎都是NP問題，這一定會造成世界不少的動盪，不過往好處想，只要確立了\(NP=P\)，我們會大幅提升人類的計算力，可以拿來解很多我們現今無法解的難題，含括各領域：人工智慧、物理、醫學 ...，人類知識科技將大步的躍進。

NP-Complete 問題

當數學家試圖解決 \(NP=P\)? 問題時，導出了一個重要的概念— NP-Complete問題。1971年美國 Stephen A. Cook提出了Cook-Levin理論，這個數學理論指出任何一個NP裡面的問題都可以在 polynomial time 內，使用DTM，將之化約成「一個布林方程式是否存在解」的問題，這個被化約的問題又稱為布爾可滿足性問題（SAT），我們稱SAT問題為NP-Complete問題。

只要滿足以下兩個條件的，我們都稱之為NP-Complete：

1. 「問題」本身是一個NP問題
2. 所有的NP問題都可以用DTM在 polynomial time 內化約成為這個「問題」。

這個概念非常強大，假設我證明了SAT是P問題，就等於今天我隨便拿到一個NP問題就可以在 polynomial time 內把問題轉換成SAT，然後再用 polynomial time 把SAT解掉，所以所有的NP問題都只是P問題了，也就是\(P=NP\)，因此NP-Complete問題就是解決 \(P=NP\) 的關鍵，如果可以證明NP-Complete問題為P問題，就可以間接證明\(P=NP\)。

NP-Complete 問題不只有SAT一種，在Cook提出Cook-Levin理論的隔一年，1972年，Richard Karp將這個想法往前推進了一步，他證明了21個不同但都難解的組合數學與圖論問題為NP-Complete問題，一樣的其中的任何一種只要被證明為P問題，都可以間接證明P=NP，目前已經有更多問題被證明為NP-Complete 問題。

大家可能還會看到一個名詞叫做NP-Hard，它的定義如下，

所有的NP問題都可以用DTM在 polynomial time 內化約成為一個「問題」，這個「問題」就叫做NP-Hard Problem

所以NP-Complete問題是NP-Hard 問題的一種特例，NP-Hard 問題可以不必是NP問題，譬如停機問題就是一個NP-Hard 問題但不是一個NP問題。

後話

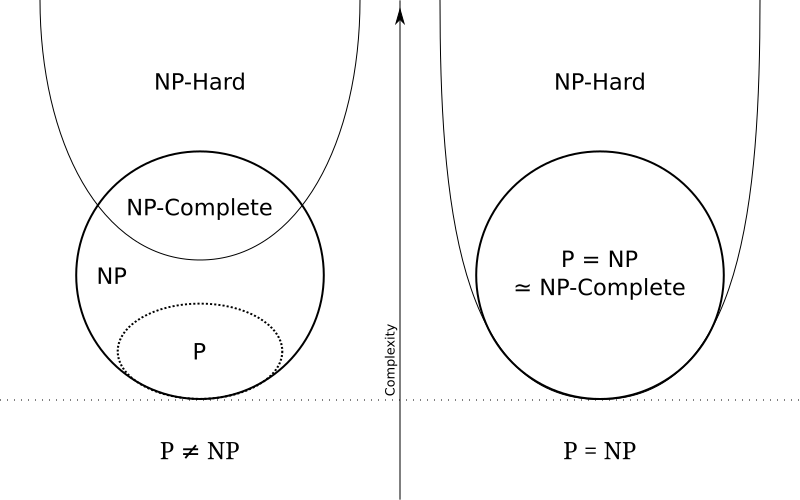
最後，以下面這張圖作個結尾，左圖是假設\(P\neq NP\)被證明的情形，NP-Hard有兩個部分，一個部分它同時是個NP問題，另外一部分則不是，所謂的NP問題就是可以用NTM在 polynomial time內給解掉的問題，另外其解的驗證必定能用DTM在 polynomial time內完成，兩種定義是等價的，有一部分的NP問題是屬於P問題，這些問題大部分都是易解的，有另外一部分的NP問題為NP-Complete問題，這些問題被視為難解的問題，我們只能用逼進的方法盡量接近答案。

右圖是假設P＝NP被證明的情形，此時NP-Complete問題已經被證明為P問題，利用NP-Complete問題的特性，我們可以化約所有NP問題為NP-Complete問題，在把這個NP-Complete問題用 polynomial time 解掉，所以P=NP=NP-Complete。

事實上，目前科學界普遍相信\(P\neq NP\)，所以遇到NP-Complete的問題，就直接標註這是一道難題，使用近似解吧！這是一個不怎麼樂觀的看法，難道說我們真的無法把這樣的難題給解決掉了嗎？也未必啦！仔細想想我們也許還有另外一個方法，只要我們創建一個NTM就可以把這些難題給解決掉啦！期待一下目前正夯的量子電腦看有沒有可能是NTM呢！？