如何辨別機器學習模型的好壞?秒懂Confusion Matrix
Posted on August 04, 2017 in AI.ML. View: 133,375
有時要鑑別一個模型的好或壞,並不能簡單的看出來,所以我們需要用一些指標去判定它的好壞,也作為我們挑選模型的依據。如果你稍微查一下有哪些指標,你就會發現指標多到讓人家眼花撩亂,一堆名詞就攤在那邊,讓人無從下手。
有一種分類問題常用的指標稱之為Confusion Matrix,這個命名很有趣,這個表格的確是很讓人感到很困惑啊!至少在看完這篇之前。Confusion Matrix是用於分類問題的一種常用的指標,它衍生很多不同的指標,下面這張圖我將Confusion Matrix畫出來,並把一些比較重要的衍生指標給標出來。

我猜想,你一定看得很模糊吧!沒關係我在這篇文章中會帶大家認識這個圖裡的各個名詞。
一開始我們從下面這個表格開始講起,這個表格就是所謂的Confusion Matrix,前面的True和False代表預測本身的結果是正確還是不正確的,而後面的Positive和Negative則是代表預測的方向是正向還是負向的。

舉iphone當例子,iphone具有指紋識別解鎖系統,假如iphone判定這個指紋是屬於使用者的,它就會解鎖,所以今天如果你按壓了,而iphone也順利解鎖了,那這種情形就屬於左上角的情況,稱為True Positive,也就是「正確的正向預測」,如果不幸的你按壓iphone,結果iphone認不得你的指紋,這就是左下角的情況,稱為False Negative,也就是「錯誤的負向預測」,接下來找你朋友一起來測試,正常情形下你朋友的指紋應該沒辦法讓iphone解鎖,這是右下角的情況,稱為True Negative,也就是「正確的負向預測」,如果令人意外的是你的朋友把你的手機解鎖了,那你最好改成用密碼鎖...,這種情況就是右上角的狀況,稱為False Positive,也就是「錯誤的正向預測」。
從上面的描述,我們當然希望我們的模型True Positive和True Negative都可以多多出現,而False Positive和False Negative可以盡量不要出現,因此這兩種狀況就稱之為Error,又各自又命名為Type I Error和Type II Error,這兩種錯誤,錯的很不一樣,如果今天指紋辨識不是放在iphone,而是放在你家大門鎖上,那你最不希望發生哪類錯誤?當然是Type I Error,也就是False Positive,此時機器會把陌生人當成主人的開門,這是我們不想看到的,我們寧可被關在門外(Type II Error)!但如果今天這個辨別系統是用在Google廣告,Google Ad會預測一個產品的潛在客戶,並做廣告投放,這個時候反而是較不希望Type II Error發生,也就是False Negative,這叫做寧可錯殺一百個也不要放過一個潛在客戶。所以下次在訓練你的模型時想清楚你不想要Type I Error還是Type II Error (鰲拜:我全都要...),並且用一些方法來放掉另一種錯誤,來降低這個我們不希望發生的錯誤。
Confusion Matrix還有衍生很多形形色色的指標,我接下來就一一的介紹。
我們把所有正確的情況,也就是True Positive和True Negative,把它加總起來除上所有情形個數,那就是Accuracy,這也是最常用的指標,但是在某些情形下這個指標會失效,如果今天實際正向的例子很少,譬如有一個信用卡盜刷偵測機器人,看了一個月的信用卡紀錄,其中真正是盜刷的資料筆數是相當少的,那我只要簡單一步來設計我的模型就可以使它Accuracy達到99%以上,你猜到了嗎?那就是通通預測沒有盜刷的情況發生,所以顯然我們需要別種指標來應對這種情況。
Precision(準確率)和Recall(召回率)這個時候就派上用場了,Precision和Recall同時關注的都是True Positive(都在分子),但是角度不一樣,Precision看的是在預測正向的情形下,實際的「精準度」是多少,而Recall則是看在實際情形為正向的狀況下,預測「能召回多少」實際正向的答案。一樣的,如果是門禁系統,我們希望Precision可以很高,Recall就相較比較不重要,我們比較在意的是預測正向(開門)的答對多少,比較不在意實際正向(是主人)的答對多少。如果是廣告投放,則Recall很重要,Precision就顯得沒這麼重要了,因為此時我們比較在意的是實際正向(是潛在客戶)的答對多少,而相對比較不在意預測正向(廣告投出)答對多少。
Precision和Recall都不去考慮True Negative,因為通常True Negative會是答對的Null Hypothesis,簡單講就是最無聊的正確結果。在門禁的解鎖問題就是陌生人按壓且門不開;在廣告投放的例子中就是廣告不投,結果那個人也不是潛在客戶:在信用卡盜刷的例子,機器人認為正常的刷卡紀錄,其實也正是正常的。在通常的命題之下,實際是正向的結果是比負向少的,理所當然預測正向的結果也要比負向少,所以True Negative通常是量最多的,也是最無聊的。
補充:Null Hypothesis通常代表比較常見的情況,在統計上我們要驗證某種概念成立,我們通常會假設一個最普通的Null Hypothesis當作正常情況,然後嘗試著利用實驗數據去否定這個Null Hypothesis,舉例:你要證明一種藥物是有效的,那你要先假設一個Null Hypothesis,譬如說給患者吃個安慰劑(可能是一顆糖果),你的藥要有辦法和Null Hypothesis產生顯著的差異,你才能證明你的藥是有效的。所以用在機器學習的例子當中,通常會把最普通的情況當作Negative,也就是當作Null Hypothesis來看待。
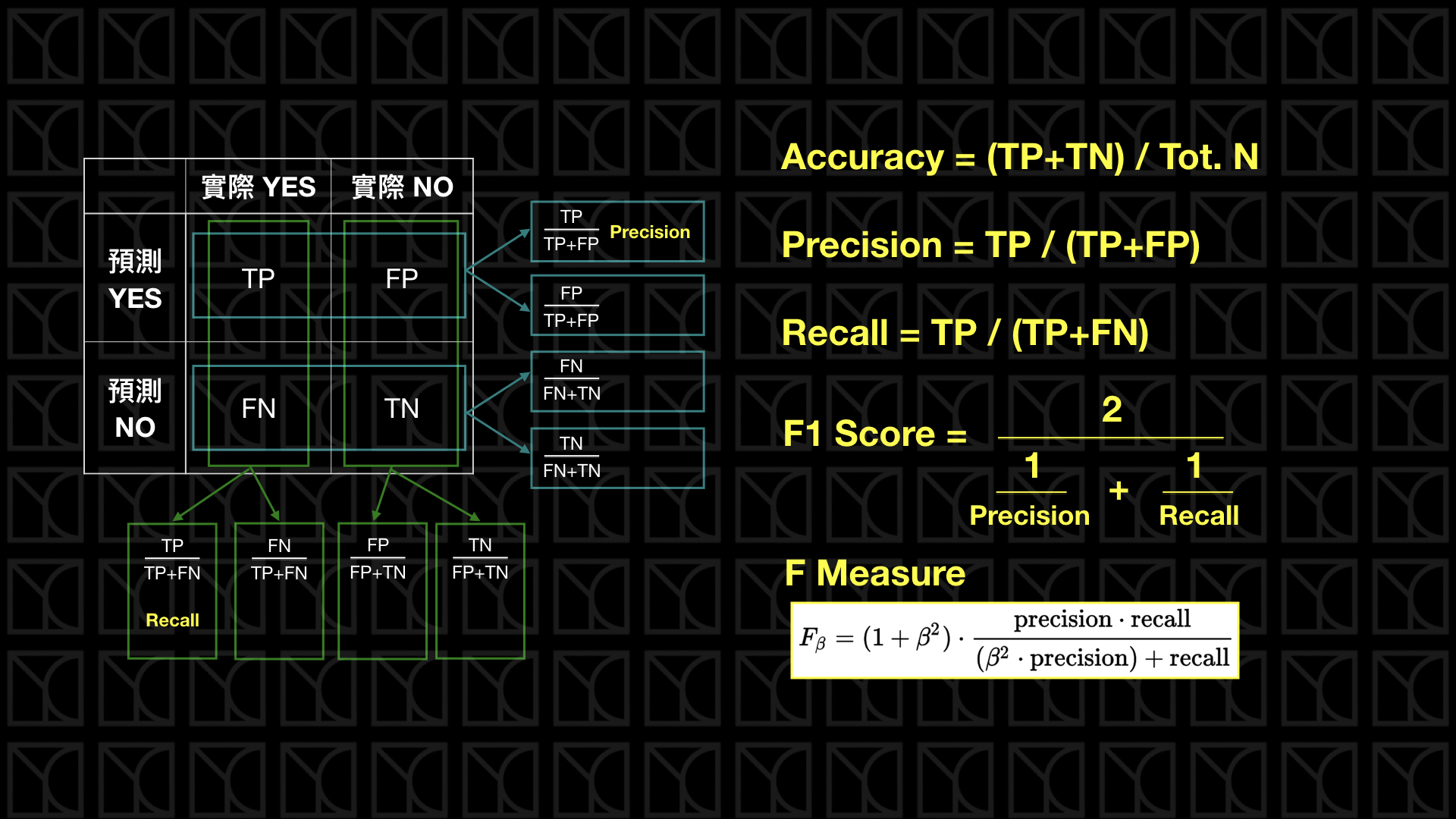
如果今天我覺得Precision和Recall都同等重要,我想要用一個指標來統合標誌它,這就是F1 Score或稱F1 Measure,它是F Measure的一個特例,當belta=1時就是F1 Measure,代表Precision和Recall都同等重要,那如果我希望多看中一點Precision,那\(belta\)就可以選擇小一點,當\(belta=0\)時,F Measure就是Precision;如果我希望多看中一點Recall,那belta就可以選擇大一點,當belta無限大時,F Measure就是Recall。
如果你仔細看F1 Measure,你會發現它的平均方法是「調和平均」,帶大家go-through三種平均方法,你就能明白為什麼要使用調和平均了。下圖列出了三種平均方法的使用時機,我們要去了解資料或數列的特性,我們才能知道要採取哪種平均方法較為恰當,大多情況算數平均都可以使用,因為我們都假設有線性關係存在,譬如說平均距離;幾何平均常用於人口計算,因為人口增加是成比例增加的;調和平均常用於計算平均速率,在固定距離下,所花時間就是平均速率,這數據成倒數關係,而F1 Measure也同樣是這樣的數據特性,在固定TP的情況下,有不同的分母,所以這裡使用調和平均較為適當。

下圖的名詞看一下有印象就好。
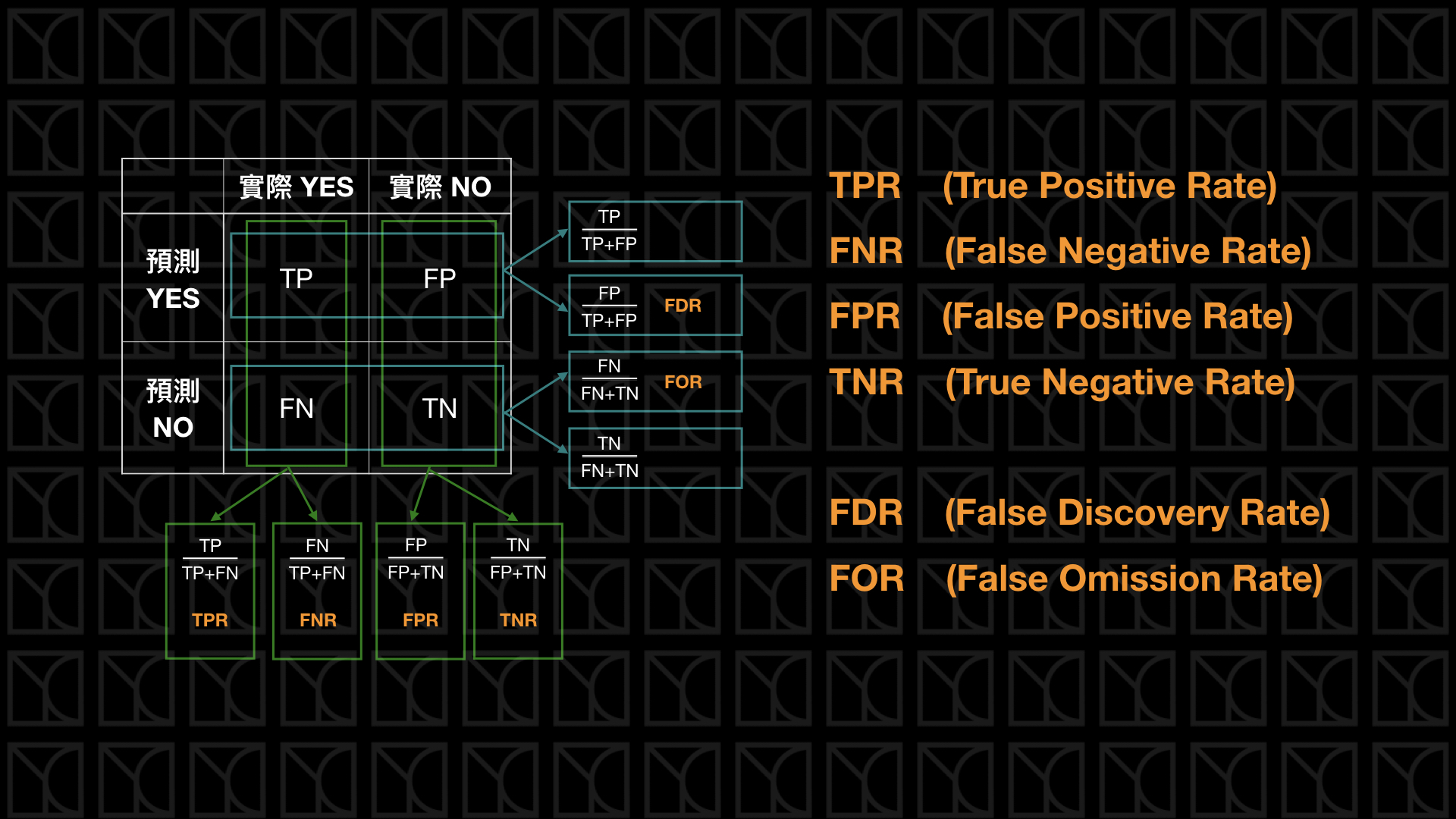
最後這頁來講一下醫學上常用的指標,首先是Prevalence(盛行率),如果以人口當作所有的樣本,實際得病的患者所佔的比例就代表這個病的盛行情況。
如果今天有一個診斷方法可以判定病人是否有得此病,有兩個指標可以看,那就是Sensitivity和Specificity,Sensitivity就是Recall,它代表的是診斷方法是否夠靈敏可以將真正得病的人診斷出來,其實就是真正有病症的患者有多少可以被偵測出來,而Specificity則代表實際沒病症的人有多少被檢驗正確的。兩種指標都是越高越好。
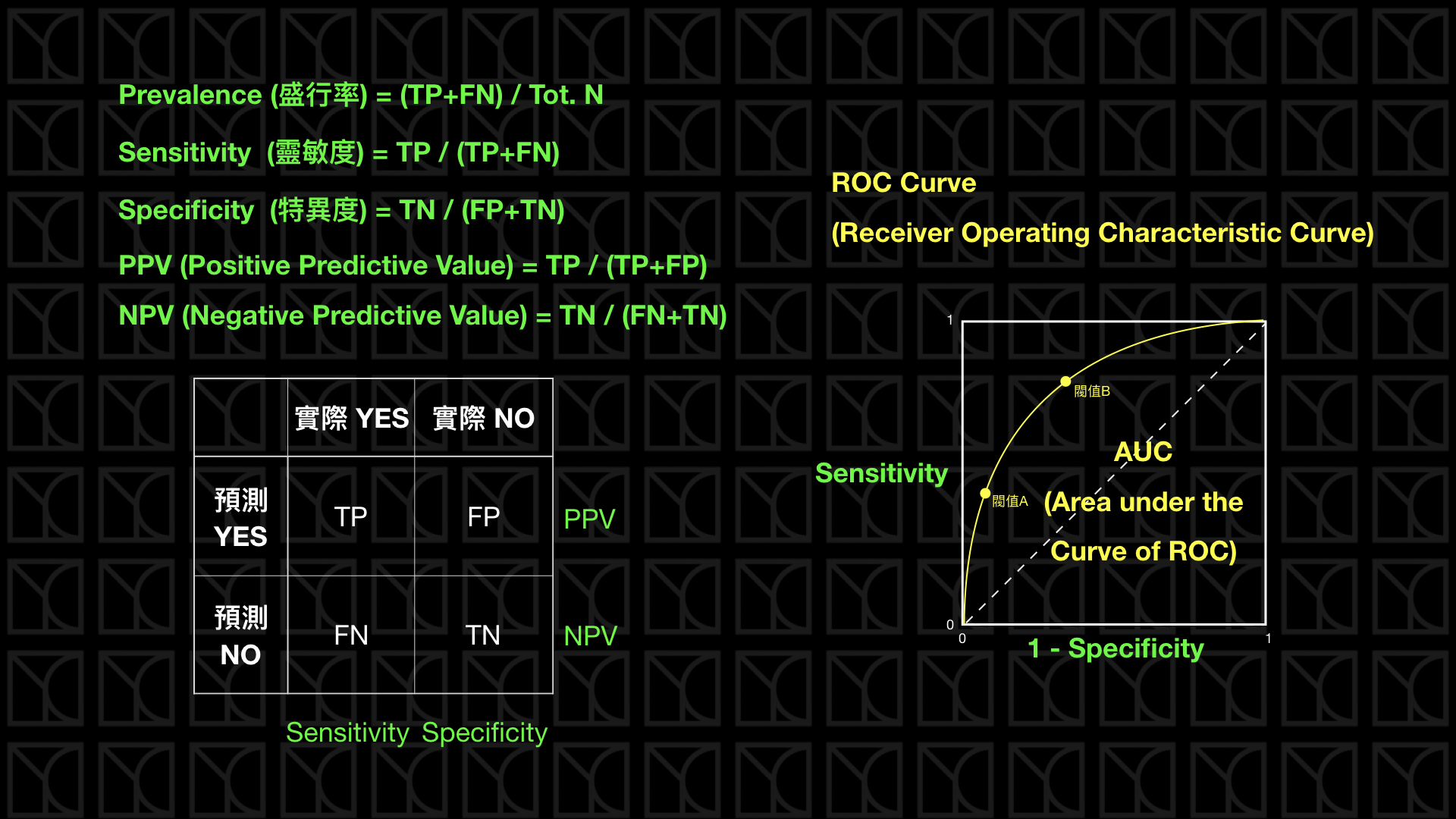
通常在醫學上,會通過一些閥值來斷定病人是否有得此病,而這個閥值就會影響Sensitivity和Specificity,這個不同閥值Sensitivity和Specificity的分布情況可以畫成ROC Curve,而ROC Curve底下的面積稱為AUC,AUC越大越好。
想必這個時候你再回去看第一張圖就更加了解了,有了這些指標,我們就多一把尺來評斷我們的分類模型究竟是做的好還是不好。