機器學習技法 學習筆記 (3):Kernel Regression
Posted on March 15, 2017 in AI.ML. View: 6,646
在上一篇當中我們看到了Kernel Trick的強大,我們繼續運用這個數學工具在其他的Regression上看看。
Soft-Margin SVM其實很像L2 Regularized Logistic Regression
上一篇中提到的Soft-Margin SVM其實很像《機器學習基石》裡頭提到的L2 Regularized Logistic Regression,如果你還記得的話,Logistic Regression是為了因應雜訊而給予每筆資料的描述賦予「機率」的性質,讓Model在看Data的時候不那麼的非黑及白,那時候有提到這叫做Soft Classification,而這個概念就非常接近於Soft-Margin的概念。
從數學式來看會更清楚,
Soft-Margin SVM:
\(min. (W^{T}W/2) + C×𝚺_{n} ξ_{n}\ \ \ s.t.\ \ \ y_{n}×(W^{T}Z_{n}+b) ≥ 1-ξ_{n}\ and\ ξ_{n} ≥ 0,\ n=1\cdots N\)
上面的式子中,可以將限制條件由max取代掉,轉換成下面的Unbounded的表示方法,
Soft-Margin SVM:
\(min. C×𝚺_{n} Err_{hinge,n} + (W^{T}W/2)\)
其中,\(Err_{hinge,n}=max[0,1-y_{n}×(W^{T}Z_{n}+b)]\),稱之為Hinge Error Measure。
接下來比較一下L2 Regularized Logistic Regression,
L2 Regularized Logistic Regression:
\(min. (1/N)×𝚺_{n} Err_{ce,n} + (λ/N)×W^{T}W\)
其中,\(Err_{ce,n}=ln[1+exp(-y_{n}×(W^{T}Z_{n}))]\),為Cross-Entropy Error Measure。
你會發現Soft-Margin SVM和L2 Regularized Logistic Regression兩個式子的形式是很接近的,都有\(W^{T}W\)這一項,只是意義上不同,在Soft-Margin SVM裡頭\(W^{T}W\)所代表的是反比於空白區大小距離的函式,而在L2 Regularized Logistic Regression裡頭則是指Regularization。
另外,我們來疊一下\(Err_{hinge,n}\)和\(Err_{ce,n}\)來看看這兩個函數像不像,
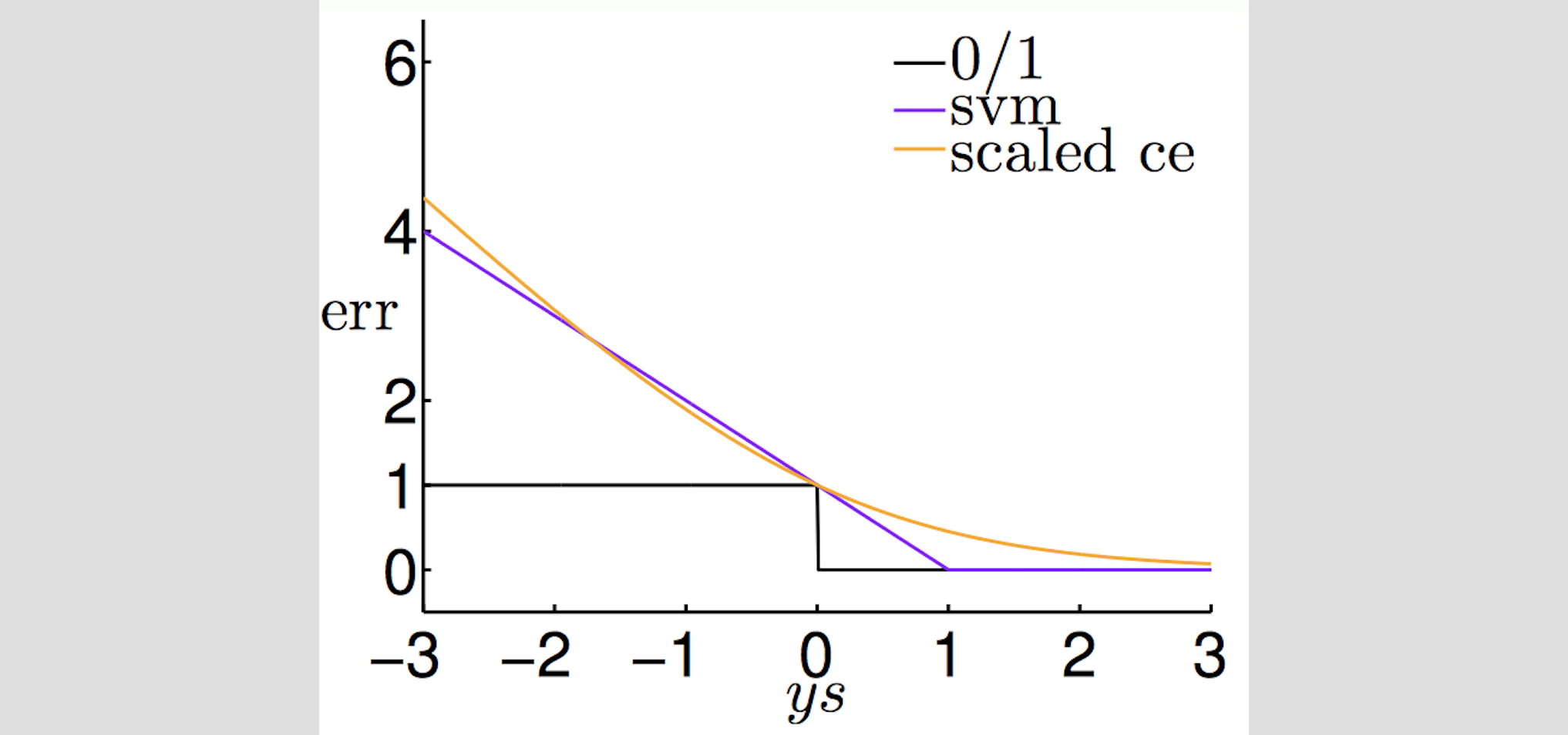
from: https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/205_handout.pdf
\(Err_{hinge,n}\)和\(Err_{ce,n}\)是非常接近的,所以我們可以說做Soft-Margin SVM,很像是在做L2 Regularized Logistic Regression。
雖然說Soft-Margin SVM和L2 Regularized Logistic Regression非常的像,但是我在做完Soft-Margin SVM後,仍然沒辦法像Logistic Regression一樣得到一個具有機率分布的Target Function,以下提供了兩種方法,第一種是間接的方法,使用兩階段學習來達成Logistic的效果;第二種是直接將L2 Regularized Logistic Regression加入有如Soft-Margin SVM的Kernel性質。
使用SVM做Logistic Regression:Probabilistic SVM
要讓Soft-Margin SVM在最後呈現的Target Function時具有機率性質,最簡單的作法就是透過兩階段的學習來達成,第一階段先用Soft-Margin SVM去解出切分資料的平面,第二階段再將Logistic Function套在這個平面上,並做Fitting,最後我們就得到一個以Logistic Function表示的Target Function,這個稱之為Probabilistic SVM。實際操作方法如下:
- 使用Soft-Margin SVM解出切平面\(W_{SVM}^{T}Z+b_{SVM}=0\),並將所有Data進一步的轉換到 \(Z'_{n}=W_{SVM}^{T}Z(X_{n})+b_{SVM}\)。
- 接下來用轉換後的結果\(\{Z'_{n},\ y_{n}\}\)做Logistic Regression得到係數A和B。
- 最後的Target Function就是 \(g(x)=Θ(A\cdot (W_{SVM}^{T}Z(X_{n})+b_{SVM})+B)\),\(Θ\)為Logistic Function。
上面的方法有一個缺點,就是如果B的值不接近0時,SVM的切平面就會和Logistic Regression的邊界就會不同,而且一個Model要Fitting兩次也相當的麻煩,以下還有另外一個可以達到一樣的具有機率性質的效果的方法—Kernel Logistic Regression。
Kernel Trick的真正精髓:Representer Theorem
在說明Kernel Logistic Regression之前我們先來複習一下Kernel的概念,並且從中將他的重要觀念萃取出來。
再來看一眼我們怎麼解Kernel Soft-Margin SVM的,
Kernel Soft-Margin SVM:
在\(0 ≤ α_{n} ≤ C;\ 𝚺_{n} α_{n}y_{n} = 0\)的限制條件下,求解\(min. [(1/2)𝚺_{n}𝚺_{m} α_{n}α_{m}y_{n}y_{m}K(X_{n},X_{m})-𝚺_{n} α_{n}]\)
得到\(α_{n}\),然後
\(W = 𝚺_{n} α_{n}y_{n}Z_{n}\)
\(b=y_{sv}-𝚺_{n} α_{n}y_{n}K(X_{n},X_{sv})\)
其中W可以想成是由\(Z_{n}\)所組合而成的,而決定貢獻程度則反應在放在它前面的係數\((α_{n}y_{n})\),\(y_{n}\)決定貢獻的方向,\(α_{n}\)決定影響的程度。
數學上,有個理論Representer Theorem可以告訴我們,所有的最佳化問題中,\(W\)的最佳解都是由\(Z_{n}\)所組合而成的,以線性代數的角度,就是\(W\)由\(Z_{n}\)所展開(span),數學上表示成\(W^*=𝚺_{n} β_{n}Z_{n}\)。
這個性質為Kernel Trick提供了一個良好的基礎,每次我們只要遇到\(W^{*T}Z\)的部分,我們就可以使用Representer Theorem把問題轉換成\(W^{*T}Z=𝚺_{n} β_{n}Z_{n}Z=𝚺_{n} β_{n}K(X_{n},X)\),就可以使用Kernel Function了。
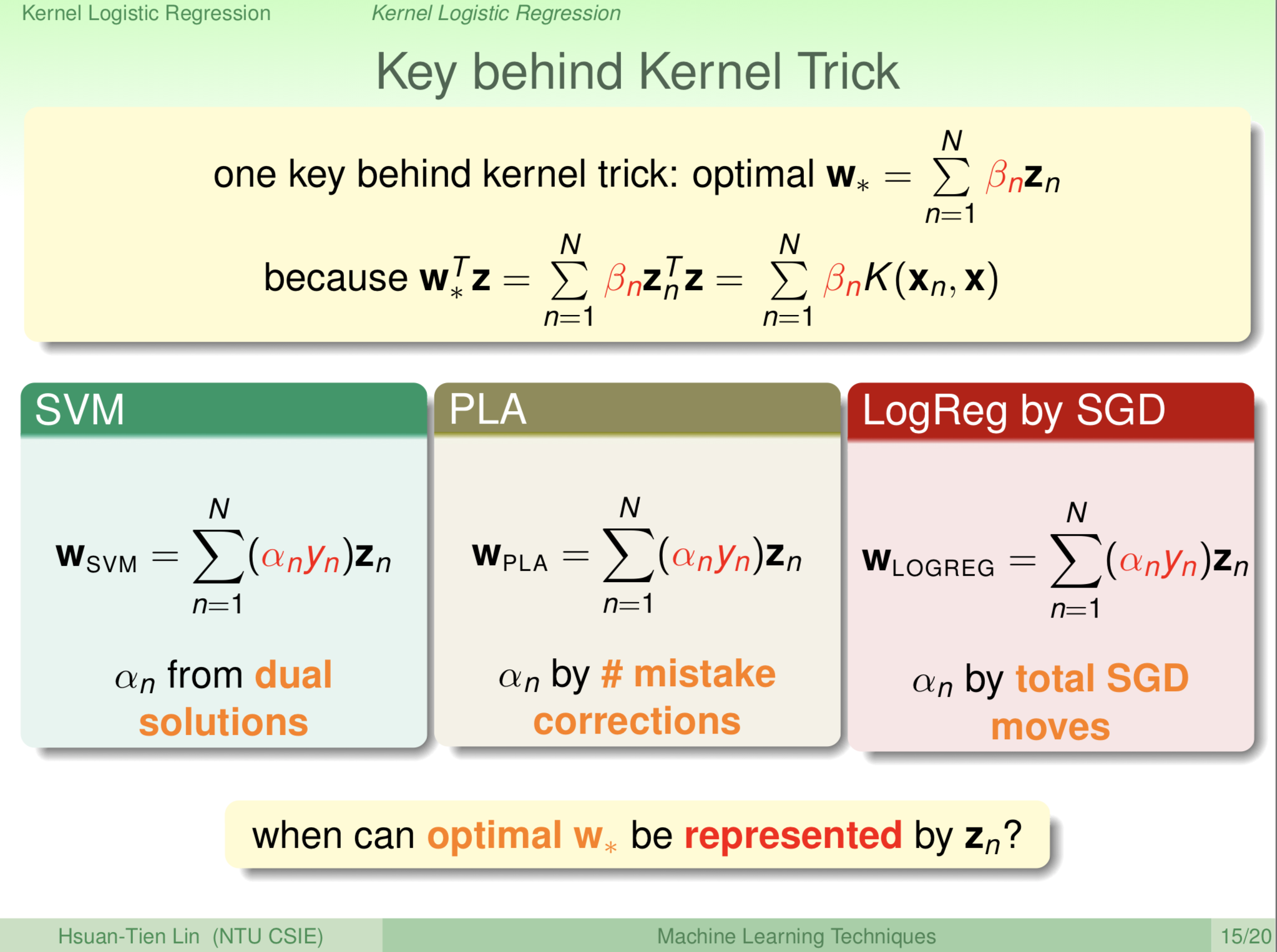
from: https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/205_handout.pdf
上圖是老師在上課時列出來SVM、PLA和Logistic Regression的W的展開式,你會發現都可以表現成Representer Theorem的形式。
有了這個概念,我們就可以把很多問題都利用Representer Theorem來轉換,並且套上Kernel Trick。
Kernel Logistic Regression
那我們有了Representer Theorem就可以直接來轉換L2 Regularized Logistic Regression,讓它有擁有Kernel的效果,
L2 Regularized Logistic Regression:
\(min. (1/N)×𝚺_{n} ln[1+exp(-y_{n}×(W^{T}Z_{n}))] + (λ/N)×W^{T}W\)
使用\(W^*=𝚺_{n} β_{n}Z_{n}\)代入得,
Kernel Logistic Regression:
\(min. (1/N)×𝚺_{n} ln[ 1+exp(-y_{n}×𝚺_{n} β_{n}K(X_{n},X)) ] + (λ/N)×𝚺_{n}𝚺_{m} β_{n}β_{m}K(X_{n},X_{m})\)
上面的式子可以使用Grandient Descent來求解\(β_{n}\),進而得到\(W^*=𝚺_{n} β_{n}Z_{n}\)。而且在Kernel Function的幫助之下,我們更容易可以做到非常高次的特徵轉換。
Kernel Ridge Regression
同理,我們也可以把相同技巧套用到Ridge Regression,
Ridge Regression:
\(min. (1/N)×𝚺_{n} (y_{n}-W^{T}Z_{n})^{2} + (λ/N)×W^{T}W\)
使用\(W^*=𝚺_{n} β_{n}Z_{n}\)代入得,
Kernel Ridge Regression:
\(min. (1/N)×𝚺_{n} (y_{n}-𝚺_{m} β_{m}K(X_{n},X_{m}))^{2} + (λ/N)×𝚺_{n}𝚺_{m} β_{n}β_{m}K(X_{n},X_{m})\)
上面的式子也可以使用Grandient Descent來求解\(β_{n}\)。
另外,這個式子有辦法推出解析解,先把上式可以寫成矩陣形式,
Kernel Ridge Regression:
\(min. E_{aug}\)
\(E_{aug}=(1/N)×(β^{T}K^{T}Kβ-2β^{T}K^{T}y+y^{T}y) + (λ/N)×β^{T}Kβ)\)
所以,由\(∇E_{aug}=0\)就可以得到最小值成立的條件為
\(β^*=(λI+K)^{-1}y\)
其實這個式子非常像之前在線性模型時使用的Pseudo-Inverse,
Pseudo-Inverse:\(W=(X^{T}X)^{-1}X^{T}y\)
不過現在更為強大了,可以求得非線性模型+Regularization下的解析解。
我們可以使用Kernel Ridge Regression來做分類問題,稱之為Least-Squares SVM (LSSVM) 。
Support Vector Regression (SVR)
其實,不管是Kernel Logistic Regression還是Kernel Ridge Regression,這種直接套用Representer Theorem在Regression上的都有一個缺點。
那就是它們的\(β_{n}\)並不確保大多數是0,如果Data筆數非常多的話,這在計算上會是一種負荷。在之前我們討論Kernel SVM時有提到只有Support Vector的數據才會對Model最後的結果有所貢獻,Support Vector的\(α_{n}>0\);而不是Support Vector的數據則沒有貢獻,Non-Support Vector的\(α_{n}=0\)。所以你可以想見的是,\(α_{n}\)大多數是0除了Support Vector外,我們稱這叫做「Sparse \(α_{n}\)」性質,有這樣的性質可以大大的減少計算量。
因此接下來我們打算讓Regression具有Support Vector的性質,稱之為Support Vector Regression (SVR)。
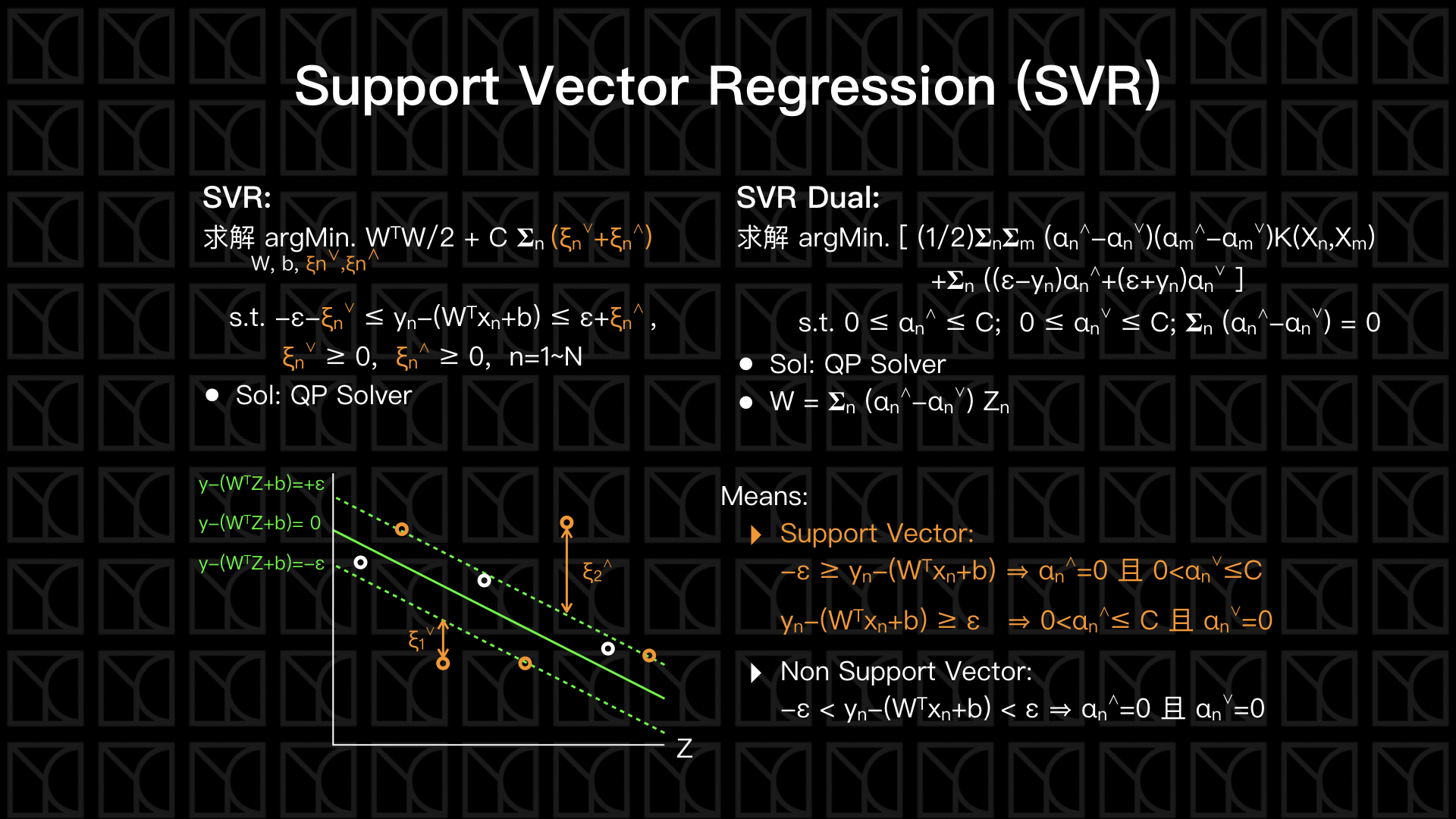
見上圖說明,Support Vector Regression簡稱SVR,以往的Linear Regression是求一條擬合直線能使所有數據點到直線的Error最小,而現在我們賦予它Soft-Margin的能力,SVR將擬合直線向外擴張距離ε,在這個擴張的區域裡頭的數據點不去計算它的Error,只有在超出距離ε外的才去計算Error,此時這個擬合直線有點像一條水管,水管外我們才計算Error,所以又稱之為Tube Regression。
這個概念和Soft-Margin SVM有點像,都是在邊界給予犯錯的機會,不同的是Soft-Margin SVM因為是分類問題,所以不允許錯誤的數據超過界,所以評估Error的方向是向內的,而SVR是向外評估Error,在水管外部上方的Error我們記作\(ξ_{n}^{⋀}\),在水管外部下方的Error我們記作\(ξ_{n}^{⋁}\),所以SVR的目的就是在Regularization之下使得\(ξ_{n}^{⋀}+ξ_{n}^{⋁}\)最小,並且調整距離ε和C來決定對Error的容忍程度。
這個問題同樣的可以化作Dual問題,問題變成只需要最佳化\(α_{n}^{⋀}\)和\(α_{n}^{⋁}\),再使用最佳化後的\(α_{n}^{⋀}\)和\(α_{n}^{⋁}\)就可以得到\(W\)和\(b\)。其中\(W=𝚺_{n} (α_{n}^{⋀}-α_{n}^{⋁}) Z_{n}\)這式子裡頭隱含著Representer Theorem,每筆數據的貢獻程度\(β_{n}=(α_{n}^{⋀}-α_{n}^{⋁})\),因此在管子內的\(α_{n}^{⋀}=0\)且\(α_{n}^{⋁}=0\),不會有所貢獻,這使得SVR具有Sparse的性質,可以大大的減少計算。
結語
這一篇中,我們一開始揭露了「Soft-Margin SVM其實很像L2 Regularized Logistic Regression」的這個現象,所以在SVM中最小化\(W^{T}W\)有點像是Regression中的Regularization,也因為形式上相當的接近,所以在SVM裡頭用到的數學技巧同樣的可以套到這些有Regularized的Regression上。
然後,我們從Kernel Soft-Margin SVM中萃取出Kernel Trick的精華—Representer Theorem,最佳化的W可以由Data的Feature \(Z_{n}\)所組成,記作\(W^*=𝚺_{n} β_{n}Z_{n}\),這提供了Kernel Trick背後的實踐基礎,接下來我們就開始運用Representer Theorem在L2 Regularized Logistic Regression和Ridge Regression上,讓這些Regression可以輕易的做非線性特徵轉換。
最後,我們指出了直接套用Representer Theorem在Regression上的缺點就是參數並不Sparse,所以造成計算量大大增加。因此Support Vector Regression (SVR)參照Soft-Margin SVM的形式重新設計Regression,並且使用Dual Transformation和Kernel Function來轉化問題,最後SVR就具有Sparse的特性了。
上一篇跟這一篇,談的是「Kernel Models」,在這樣的形式下我們可以讓我們的「特徵轉化」變得更為複雜,甚至是無窮多次方還是做得到的。下一篇,我們會進到另外一個主題—Aggregation Models。