機器學習技法學習筆記 (2)：Support Vector Machine (SVM)

Posted on February 20, 2017 in AI.ML. View: 11,884

在上一篇文章當中，我們掃過了《機器學習技法》將會包含的內容，今天我們正式來看SVM。

如果我想要使用無窮次高次方的非線性轉換加入我的Model，可以做到嗎？上一篇，我告訴大家，只要使用Dual Transformation加上Kernel Function等數學技巧就可以做到，我們今天就來看一下這是怎麼一回事。

本篇文章分為兩個部分，第一部分我盡量不牽扯太多數學計算，而將數學證明放在第二個部分，數學證明的部分非常複雜，但我並不打算把它們忽略掉，因為這些數學計算是相當重要的，它所帶來的方法和概念是可以重複使用的，也有助於你了解和創造其他演算法，所以有心想要成為專家的你請耐心的把後半段的數學看完。

Hard-Margin Support Vector Machine (SVM)

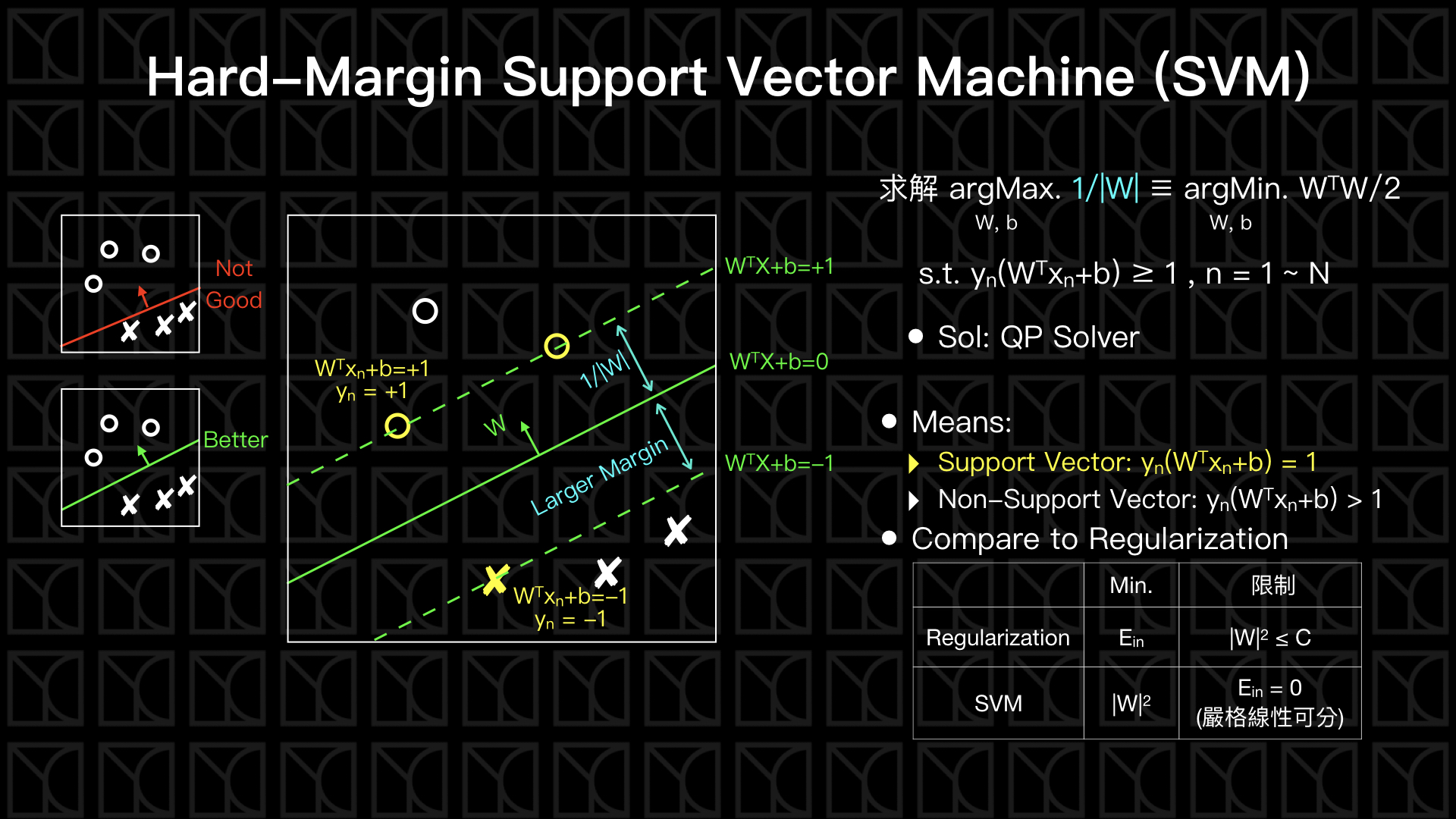
Hard-Margin SVM

回到我們最熟悉的二元分類問題，如果問題的答案是線性可分的話，我們可以找到一條直線把兩類Data給切開來，而在以前PLA的方法，切在哪裡其實是沒辦法決定的，PLA只能幫你找到可以分開兩類的一刀，但不能幫你把這刀切的更好。

我們希望這個切開兩類的邊界可以離兩類Data越遠越好，讓邊界到Data有一個較大的空白區，這就是Hard-Margin SVM做的事。

我們先來看一下如何計算切平面到任意Data的距離，首先我先假設切平面的方程式為

$$ W^T X+b = 0 (切平面) $$

回想一下高中數學，這個平面的法向量是W，垂直於平面，所以垂直於平面的單位法向量是 $W/|W|$，今天如果我有一點Data Point落在$X$，另外在平面上任意再找一點$X_0$，從$X_0$到$X$的向量表示為$X-X_0$，這個向量如果投影到單位法向量上，這個向量的大小正是Data Point到平面的最短距離，表示成

$$ d = |W\cdot (X - X_0)| / |W| $$

$X_0$符合切平面的方程式$W^T X_0+b = 0$代入，得

$$ d = |W\cdot X + b| / |W| $$

所以假如我有一群線性可分的二元分類Data，這個切平面我希望可以離兩類Data越遠越好，所以我會有一段全部都沒有Data的空白區，這邊假設這個空白區的邊界為

$$ W^TX+b = ±1 $$

這個假設是可以做到的，因為我們可以以比例去調整$W$和$b$來達到縮放的效果，而不會影響切平面$W^T X+b = 0$ 。從上面的距離公式，我們知道在這個假設之下，空白區邊界距離切平面為

$$ margin = 1 / |W| $$

而剛好落在這空白區邊界的Data會符合以下方程式

$y_n\times (W^T X_n+b) = 1\ (Support\ Vector)$

$y_n$的正負剛好和$(W^T X_n+b)$相抵消，這些落在空白區邊界的Data被稱為Support Vector，就字面上的意義就像是空白區由這一些數據給「撐」起來，而切平面只由這些Support Vector的數據點所決定，和其他的數據點無關。

如果考慮所有Data的話，應該要滿足

$$ y_n\times (W^T X_n+b) ≥ 1\ (All\ Data) $$

綜合上述，Hard-Margin SVM的目標就是，在符合$y_n\times (W^T X_n+b) ≥ 1 ,\ n=1~N$的條件下，求$Margin (1 / |W|)$最大的情形，也可以等價於求$(W^T W/2)$ 最小的情形，這個問題有辦法使用QP Solver來求解，詳見這裡，我就不多加介紹這個數學工具。

Kernel Function

Kernel Function是最終可以讓我們有無限多次方特徵的數學工具，但這個工具非常容易理解。

假設考慮一個非線性轉換，將$X$空間轉換到$Z$空間，那如果我需要計算轉換過的兩個新Features相乘$Z_n (X_n)\times Z_m(X_m)$，我有辦法不需要先做特徵轉換再相乘，而是直接使用原有的Features $X_n$和$X_m$求出$Z_n(X_n)×Z_m(X_m)$的最後結果？這種情形數學可以表示成$K(X_n,X_m)=Z_n(X_n)×Z_m(X_m)$，這個函式就叫Kernel Function。

如果有了Kernel Function這樣的數學工具，就可以簡化和優化因為「特徵轉換」所帶來的複雜計算。

我列出以下幾種Kernel Function：

Polynomial Kernel：$K_Q(X_n,X_m)=(ζ+γ X_n^T X_m)^Q$等價於「Q次方非線性轉換後的兩個新特徵相乘」。
Guassian Kernel：$K(X_n,X_m)=exp(-γ|X_n-X_m|^2)$等價於「無窮次方非線性轉換後的兩個新特徵相乘」。

因此有了Guassian Kernel的幫忙，我們完全不需要管特徵轉換有多複雜，我們可以直接使用原有的Features 來計算「無窮次方的非線性轉換」。

最後給予Kernel Function一個物理解釋，Kernel Function說穿了就是兩個向量轉換到Z空間後的「內積」，「內積」可以約略想成是「相似程度」，當兩個向量同向，內積是正的，相似度高，但當兩個向量反向，內積是負的，相似度極低，所以你會發現Guassian Kernel在$X_n=X_m$會出現最大值，因為代表這兩個位置相似度極高。

Kernel Hard-Margin SVM

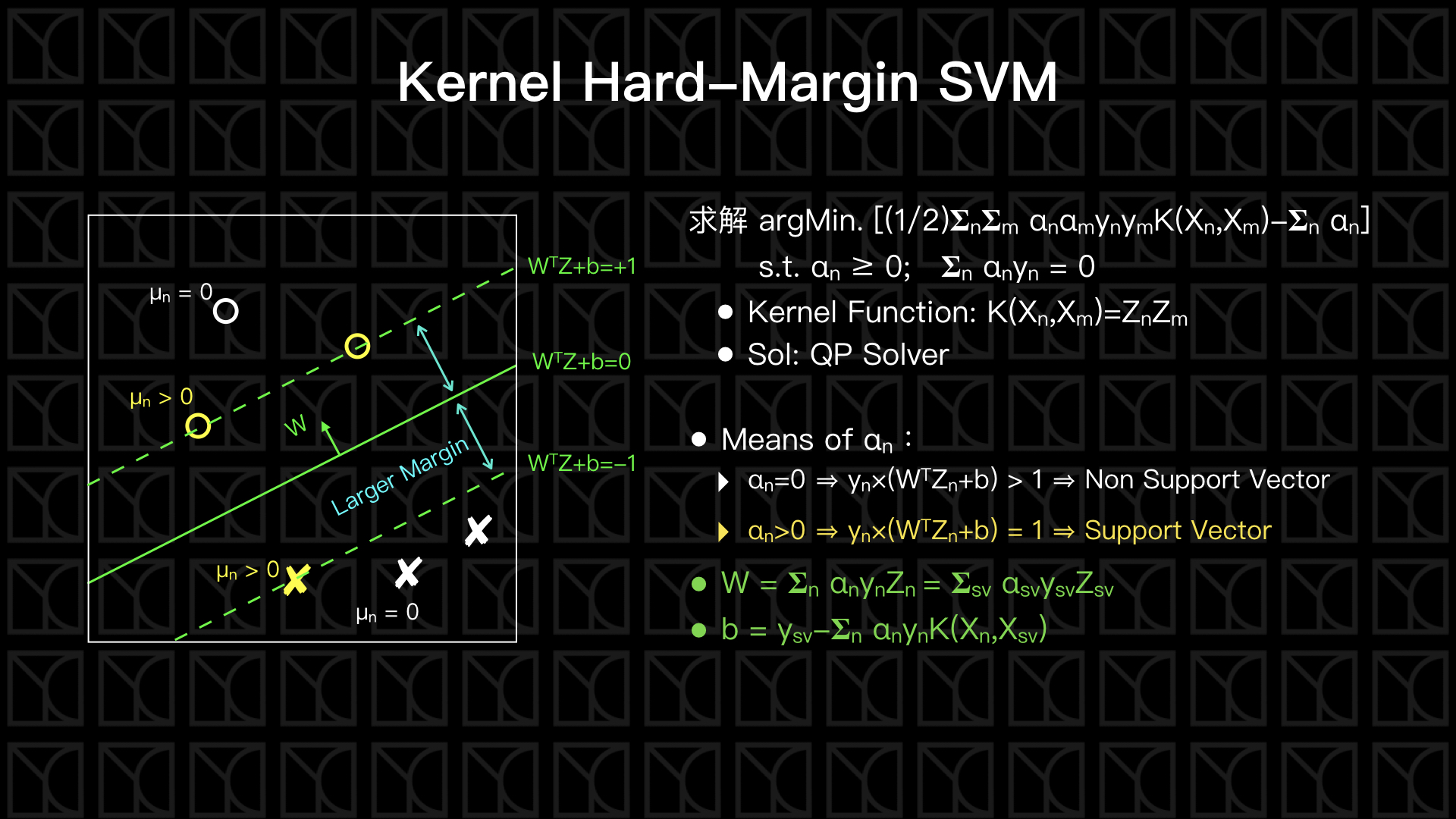
那我們如何使用Kernel Function來使得Hard-Margin SVM更厲害呢？我們必須額外引入另外的數學工具，包括：Lagrange Multiplier和Lagrange Dual Problem，才有辦法把Kernel Function用上，不過這部份的數學有一些複雜，我將這部份的證明放在後面的附錄上，這邊就直接從結果講起。

Kernel Hard-Margin SVM的公式是，在$α_n ≥ 0; 𝚺_n α_n y_n = 0$的限制條件下，求解$α_n$

使得 $[(1/2)𝚺_n 𝚺_m α_n α_m y_n y_m K(X_n,X_m)-𝚺_n α_n]$為最小值，

其中$K(X_n,X_m)$就是Kernel Function，由你的特徵轉換方式來決定，這個問題一樣可以使用QP Solver來求解。

當我們已經有了每筆數據點的$α_n$了，接下來可以利用$α_n$求出切平面的W和b，在那之前來看一下$α_n$的意義，$α_n$可以看作是某個數據點對切平面的貢獻程度，$α_n=0$的這些數據點為非Support Vector，而$α_n>0$的這些數據點是Support Vector，所以對切平面有貢獻的只有Support Vector而已，這和剛剛的結論相同。因此，W和b可由Support Vector決定，

$W = 𝚺_{n=sv} α_n y_n Z_n$

$b=y_{sv}-𝚺_n α_n y_n K(X_n,X_{sv})$

最後提一個非常重要的概念，是什麼原因讓我們不需要管特徵轉換的複雜度？以往我們的作法是這樣的，我們有每筆Data的Features，接下來對每筆Data做特徵轉換，然後在用特徵轉換後的新Features去Train線性模型，這麼一來如果特徵轉換的次方非常高的話，計算的複雜度就會全落在特徵轉換上。所以我們巧妙的使用數學工具，讓我們可以單單使用Data的Labels來做優化，而將複雜的特徵轉換利用Kernel Function的方式「嵌入」到優化的過程裡頭，此時計算量就只與Data數量有關，所以可以完全不管特徵轉換所帶來的複雜度。

Kernel Hard-Margin SVM: 無窮次方的特徵轉換效果如何?

終於我們可以使用無窮次方的特徵轉換了，只要使用Kernel Hard-Margin SVM搭配上Guassian Kernel：$K(X_n,X_m)=exp(-γ|X_n-X_m|^2)$就可以辦到，下圖是模擬的結果，是不是看起來很強大，隨著γ的不同會有不一樣的切分方法，你會發現γ越大時看起來的結果越接近Overfitting，所以必須小心挑選γ的大小。

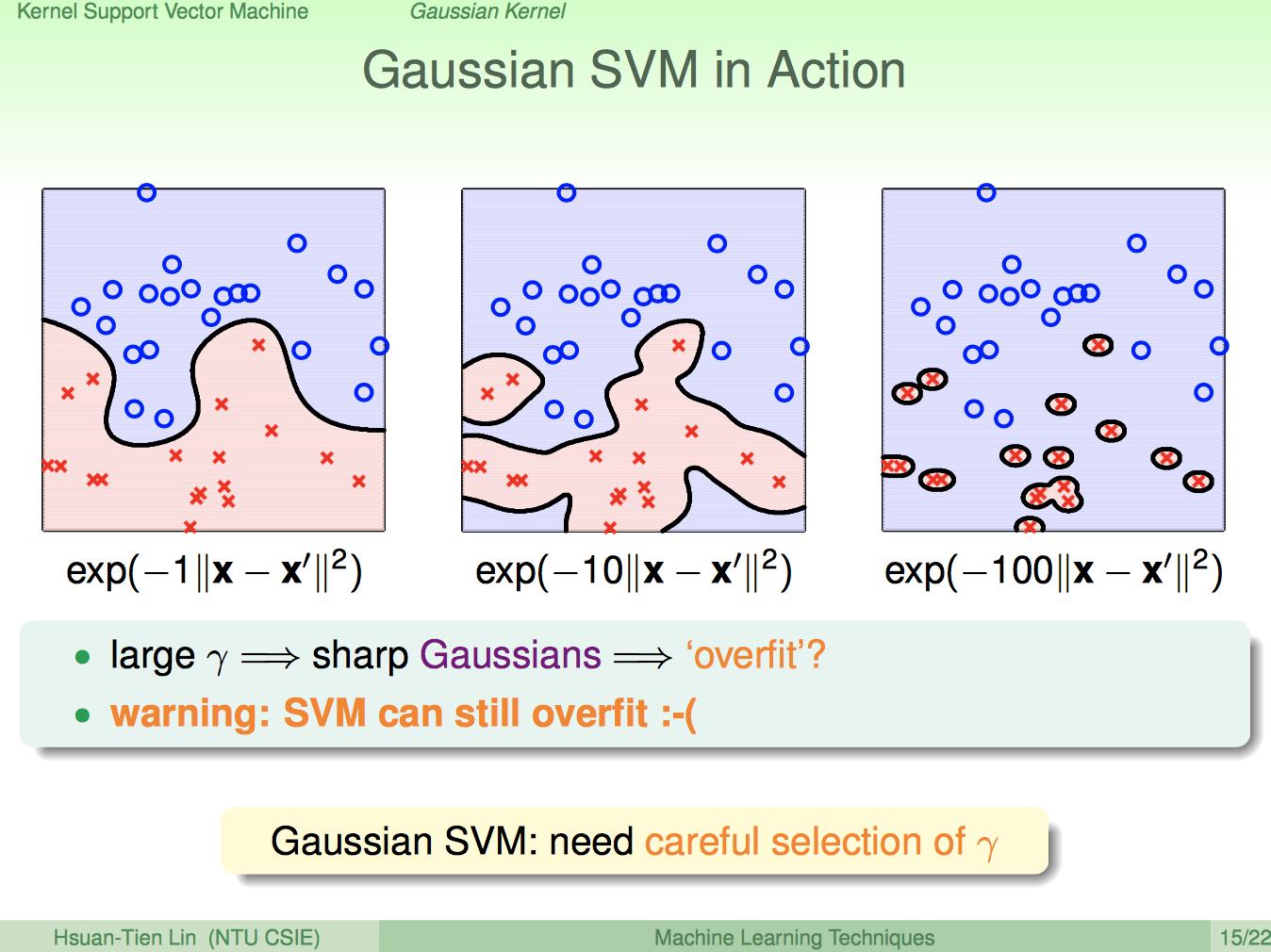
Guassian Kernel in Hard-Margin SVM

from: https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/203_handout.pdf

Soft-Margin SVM

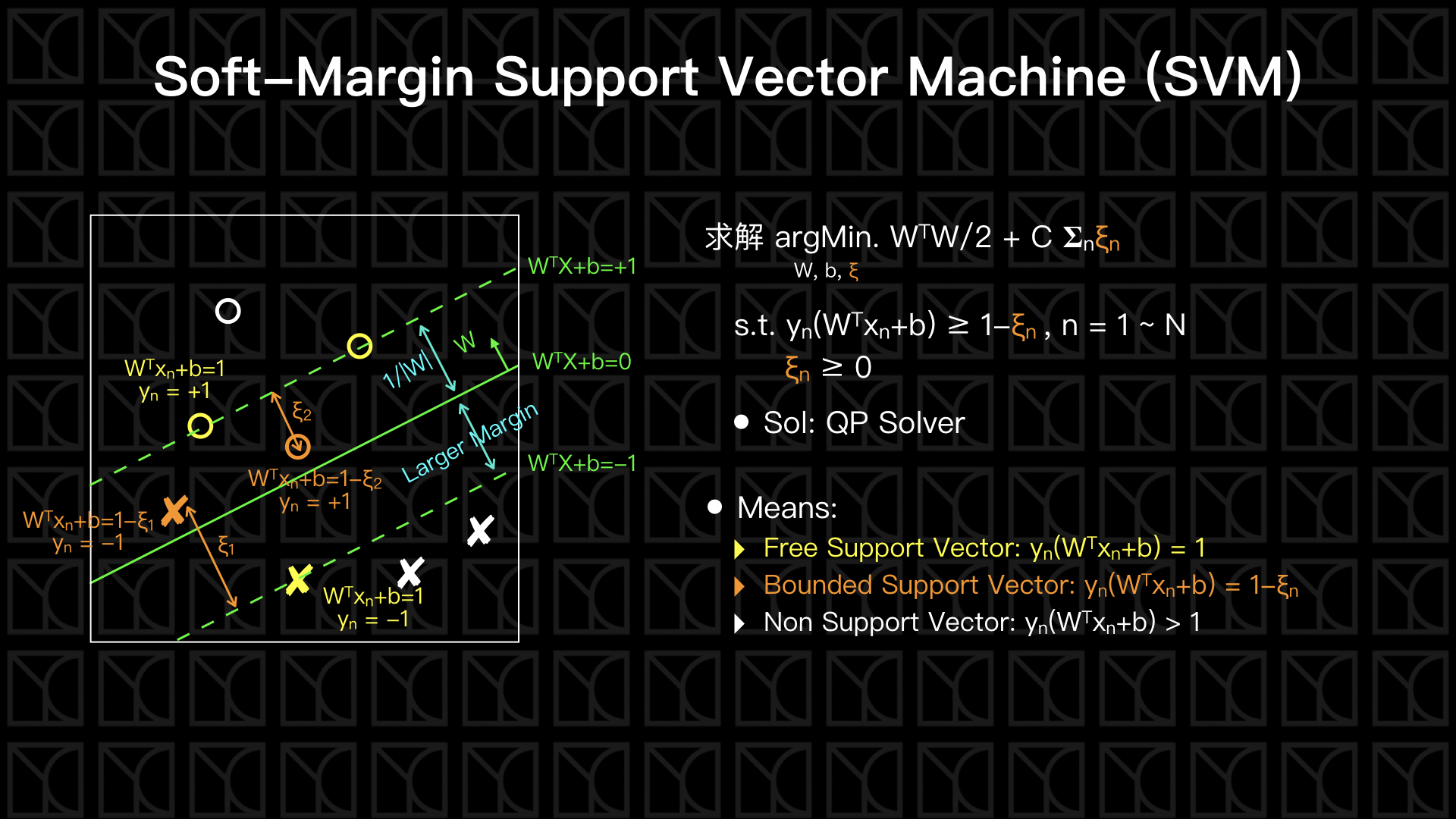
剛剛Hard-Margin SVM會很容易Overfitting的原因在於它的機制無法容忍雜訊，所以接下來要講的Soft-Margin SVM可以容忍部份的Data違反規則，讓它們可以超出空白區的邊界。

見上圖，可以發現我們稍微修改了Hard-Margin SVM，加入了參數$ξ_n$，$ξ_n$代表錯誤的Data離空白區邊界有多遠，而我們將$ξ_n$的總和加進去Cost裡面，在優化的過程中將使違反的狀況不會太多和離邊界太遠，而參數C負責控制$ξ_n$總和的影響程度，如果C很大，代表不大能容忍雜訊；如果C很小，則代表對雜訊的容忍很寬鬆。

因此我們現在有兩種Support Vector，一種是剛好落在空白區邊界的，稱為Free Support Vector；另外一種是違反規則並超出空白區的，稱為Bounded Support Vector，切平面一樣是由這些Support Vector所決定。

Kernel Soft-Margin SVM

接下來同樣的對Soft-Margin SVM做數學上Lagrange Multiplier和Lagrange Dual Problem的轉換，再將Kernel Function用上，一樣的，我將這部份的證明放在後面的附錄上，這邊就直接從結果講起。

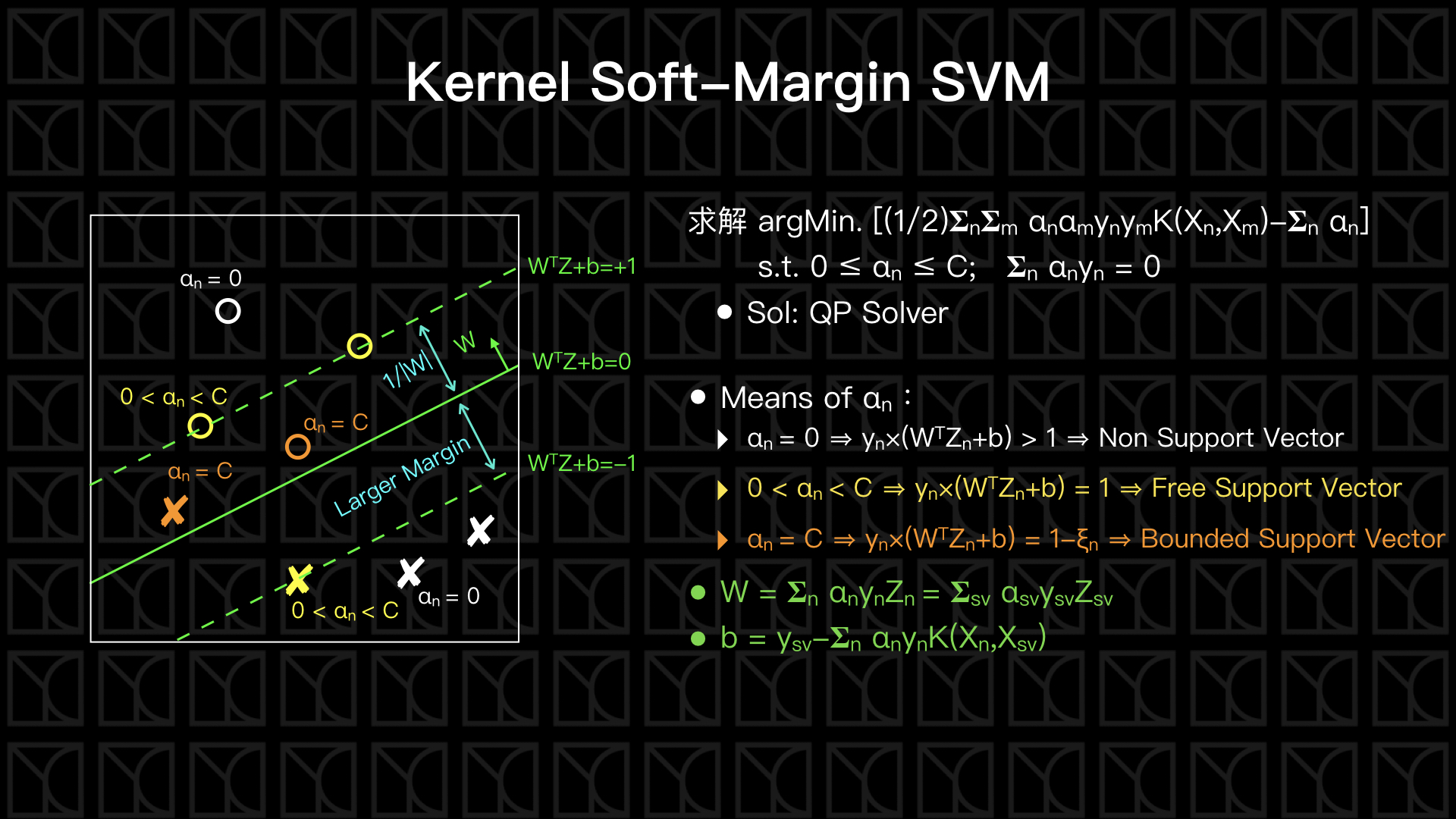
Kernel Soft-Margin SVM的公式是，在$0 ≤ α_n ≤ C;\ 𝚺_n α_n y_n = 0$的限制條件下，求解$α_n$

使得 $[(1/2)𝚺_n 𝚺_m α_n α_m y_n y_m K(X_n ,X_m)-𝚺_n α_n]$為最小值，

你會發現和Kernel Hard-Margin SVM唯一只差在$α_n$被$C$所限制。

當我們已經有了每筆數據點的$α_n$了，接下來可以利用$α_n$求出切平面的$W$和$b$，$α_n$一樣的可以看作是某個數據點對切平面的貢獻程度，$α_n=0$的這些數據點為非Support Vector，而$α_n>0$的這些數據點是Support Vector，可以進一步細分，$α_n < C$為Free Support Vector，而$α_n＝C$為Bounded Support Vector。相同的，W和b可由Support Vector (Free Support Vector和Bounded Support Vector)決定，跟Kernel Hard-Margin SVM公式一模一樣

$W = 𝚺_{n=sv} α_n y_n Z_n$

$b=y_{sv} -𝚺_n α_n y_n K(X_n,X_{sv})$

Kernel Soft-Margin SVM: 容忍雜訊的無窮次方特徵轉換

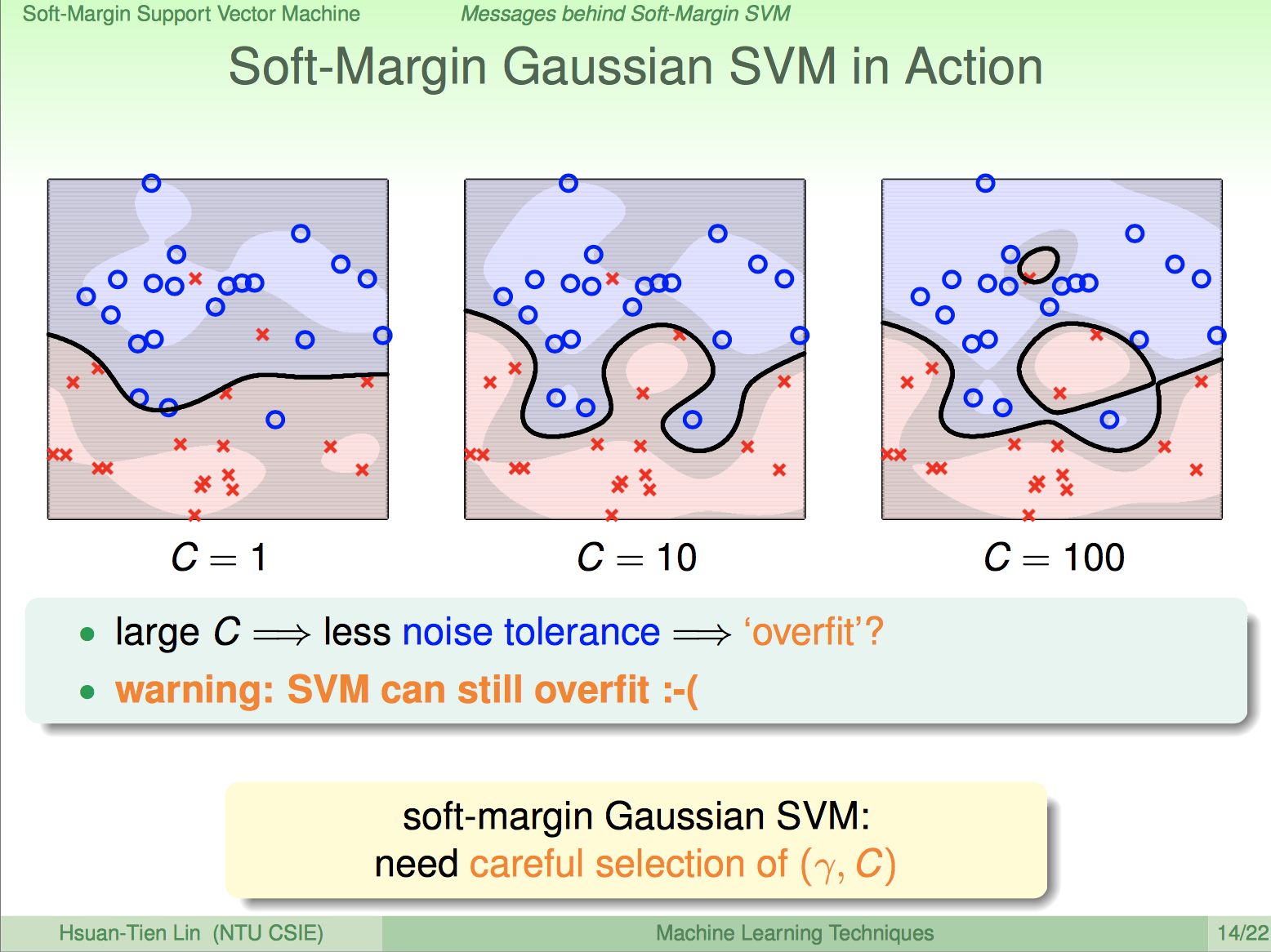
Guassian Kernel in Soft-Margin SVM

from: https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/204_handout.pdf

來看看Kernel Soft-Margin SVM搭配上Guassian Kernel的效果如何，上圖是模擬的結果，我們會發現有部分Data違反分類規則，所以Soft-Margin SVM確實可以容忍雜訊，而且$C$越小，容忍雜訊的能力越強，所以要特別注意$C$的選取，如果沒有選好還是可能造成Overfitting的。

結語

在這一篇當中，我們介紹了Hard-Margin SVM和Soft-Margin SVM，並且成功的利用數學工具將問題轉換成，可以單單使用Data的Labels來做優化，而將複雜的特徵轉換利用Kernel Function的方式「嵌入」到優化的過程裡頭，此時計算量就只與Data數量有關，所以可以完全不管特徵轉換所帶來的複雜度，因此利用Guassian Kernel就可以做到「無窮多次的特徵轉換」了。最後再次強調數學的部分非常重要，它提供的方法和概念是可以重複使用的，而這部份的數學是少不了的，所以有興趣的可以繼續往下看下去。

[進階] 拉格朗日乘子法（Lagrange Multiplier）

如果是物理系學生修過古典力學，應該對這個數學工具不陌生。Lagrange Multiplier是用在有限制條件之下的求極值問題，步驟如下：

問題：在限制 $g_i (x_1,x_2, … , x_n) = 0,\ i=1\cdots k$ 之下，求 $f(x_1,x_2, … , x_n)$ 的極值
假設Lagrange Function： $L(x_1,x_2, … , x_n,λ_i) = f(x_1,x_2, … , x_n) + 𝚺_i λ_i × g_i(x_1,x_2, … , x_n)$
聯立方程式求解：
找L的極值：$∇L = 0$ [Stationarity Condition]
$g_i (x_1,x_2, … , x_n) = 0,\ i=1\cdots k$ [Primal Feasibility Condition]
求解以上聯立方程式得到最佳解 $x_{1},x_{2}, … , x_{n}$

上面的聯立方程式不難理解，Primal Feasibility Condition就是我們的限制式，然後Stationarity Condition就是求極值的方法，非常直觀，滿足上面的式子我們就可以在限制上面找極值。

上面是一般的Lagrange Multiplier，只有考慮到限制式是等式的情形，假如限制條件是不等式呢？我們來看一下加強版的Lagrange Multiplier：

問題：在限制 $g_{i}(x_{1},x_{2}, … , x_{n}) = 0,\ i=1\cdots k$ 且 $h_{j}(x_{1},x_{2}, … , x_{n}) ≤ 0,\ j=1\cdots r$ 之下，求 $f(x_{1},x_{2}, … , x_{n})$ 的極值
假設Lagrange Function： $L(x_{1},x_{2}, … , x_{n}, λ_{i},μ_{j}) = f(x_{1},x_{2}, … , x_{n}) + 𝚺_{i} λ_{i} × g_{i}(x_{1},x_{2}, … , x_{n}) + 𝚺_{j} μ_{j} × h_{j}(x_{1},x_{2}, … , x_{n})$
聯立方程式求解：
找$L$的極值：$∇L = 0$ [Stationarity Condition]
$g_{i}(x_{1},x_{2}, … , x_{n}) = 0,\ i=1\cdots k$ 且 $h_{j}(x_{1},x_{2}, … , x_{n}) ≤ 0,\ j=1\cdots r$ [Primal Feasibility Condition]
$μ_{j} × h_{j} (x_{1},x_{2}, … , x_{n}) = 0,\ j=1\cdots r$ [Complementary Slackness Condition]
求$L$的最小值時 $μ_{j} ≥ 0,\ j=1\cdots r$；求$L$的最大值時 $μ_{j} ≤ 0,\ j=1\cdots r$ [Dual Feasibility Condition]
以上的條件包括Stationarity、Primal Feasibility、Complementary Slackness、Dual Feasibility通稱 KKT (Karush-Kuhn-Tucker) Conditions

加強版的Lagrange Multiplier和一般版的一樣有Stationarity Condition和Primal Feasibility Condition。唯一增加的是Complementary Slackness Condition和Dual Feasibility Condition。

先來講一下Complementary Slackness Condition怎麼來的，我們來考慮不等式條件$h_{j}(x_{1},x_{2}, … , x_{n}) ≤ 0$，會有兩個情形發生，一個是壓到邊界，也就是$h_{j}(x_{1},x_{2}, … , x_{n}) = 0$，這個時候問題就回到一般版的Lagrange Multiplier，此時$μ_{j}$和$λ_{i}$效果是一樣的，$μ_{j}$可以是任意值；另外一種情況是我沒壓到邊界，也就是$h_{j}(x_{1},x_{2}, … , x_{n}) < 0$，這個時候我可以把這個限制看作不存，最簡易的方法就是令$μ_{j}=0$，他在$L(x_{1},x_{2}, … , x_{n}, λ_{i},μ_{j})$ 中就不參與作用了。所以綜合壓到邊界和不壓到兩種情況，我們可以寫出一個有開關效果的方程式 $μ_{j} × h_{j}(x_{1},x_{2}, … , x_{n}) = 0$，這就是Complementary Slackness Condition。

另外一個是Dual Feasibility Condition，這個限制一樣是在不等式條件才會發生，$μ_{j}$的正負號取決於$L$是要求最大還是求最小值，稍微解釋一下，找極值我們用$∇L = 0$這個式子來求，代入Lagrange Function後得$∇L = ∇f +𝚺_{i}λ_{i}×∇g_{i}+𝚺_{j}μ_{j}×∇h_{j}=0$，先定性來看，假設不計$∇g_{i}$的影響，當最後解落在$h ≤ 0$的邊界上時$∇f＝- μ×∇h$，因為$h ≤ 0$的關係，所以$∇h$是朝向可行區的外面，如果今天是求$f$的極小值，那們$∇f$應當朝著可行區才合理，如果不是的話則可行區內部有更小更佳的解，所以求極小值時$μ ≥ 0$；如果是求$f$的極大值，那$∇f$應當朝著可行區的外面，所以$μ ≤ 0$，這個條件待會會用在對偶問題上面。

其實我們之前在《機器學習基石》裡的Regularization有偷用了Lagrange Multiplier的產物。

Regularization將W的長度限制在一個範圍，表示成

$$ |W|^{2} ≤ C $$

在這個條件下我們要找$E_{in}$的極小值，使用加強版的Lagrange Multiplier：

問題：在限制 $|W|^{2} - C ≤ 0$ 之下，求 $E_{in}$ 的極小值
假設Lagrange Function： $L = E_{in} + μ × ( |W|^{2} - C)$
聯立方程式求解：
$𝞉L / 𝞉W = 𝞉E_{in} / 𝞉W + 2μ × |W| = 0$ [Stationarity Condition]
$|W|^{2} - C ≤ 0$ [Primal Feasibility Condition]
$μ × ( C - |W|^{2} ) = 0$ [Complementary Slackness Condition]

Stationarity Condition的結果就是Regularization的結果了，可以回去參照一下。

[進階] Lagrangian Dual Problem

接下來來講對偶問題，這個部分很難，我也是反覆在網路上看了很多篇介紹才弄懂，推薦大家看這一篇，這篇介紹的很清楚，應該會對大家理解Lagrangian Dual有幫助。

來考慮一下待會會用到的求極小值問題，

在限制 $g_{i}(x_{1},x_{2}, … , x_{n}) = 0,\ i=1\cdots k$ 且 $h_{j}(x_{1},x_{2}, … , x_{n}) ≤ 0,\ j=1\cdots r$ 之下，求 $f(x_{1},x_{2}, … , x_{n})$ 的極小值。

如果我們利用剛剛的解法，稱之為Lagrangian Primal Problem。

而這個問題可以等效轉換成Lagrangian Dual Problem，利用以下關係式

$Minimum Problem ≡ min. L ≡ min. [max._{μ ≥ 0} L] ≥ max._{μ ≥ 0} [min. L(μ)]$

我們在將原本$min. L$ 換成$min. [max._{μ ≥ 0} L]$ 是不影響結果的，因為我們剛剛分析過了在求最小值時$μ ≥ 0$是合理的，相反的如果$μ < 0$，則求$max._{μ ≥ 0} L$時會產生無限大的結果，接下來就是交換$min.$和$max.$的部分，數學上可以證明$min. [max._{μ ≥ 0} L] ≥ max._{μ ≥ 0} [min. L(μ)]$這樣的關係，我們就稱左式轉到右式為Dual轉換。

而上面式子右側的求法，我們可以先求出$Θ(λ_{i},μ_{j}) =\ given\ λ_{i},μ_{j}\ to\ find\ min. L(x_{1},x_{2}, … , x_{n}, λ_{i},μ_{j})$ ，作法是使用$∇L = 0$所產生符合極值的參數代入$L(x_{1},x_{2}, … , x_{n}, λ_{i},μ_{j})$，換成以$λ_{i}$,$μ_{j}$表示的$Θ(λ_{i},μ_{j})$。然後，再求$Θ(λ_{i},μ_{j})$的最大值，就可以了。

經過Dual轉換後，我們將原本在$x_{1},x_{2}, … , x_{n}$的問題轉換到$λ_{i},μ_{j}$的空間上。

這個轉換我們可以使用下面的圖來解釋，

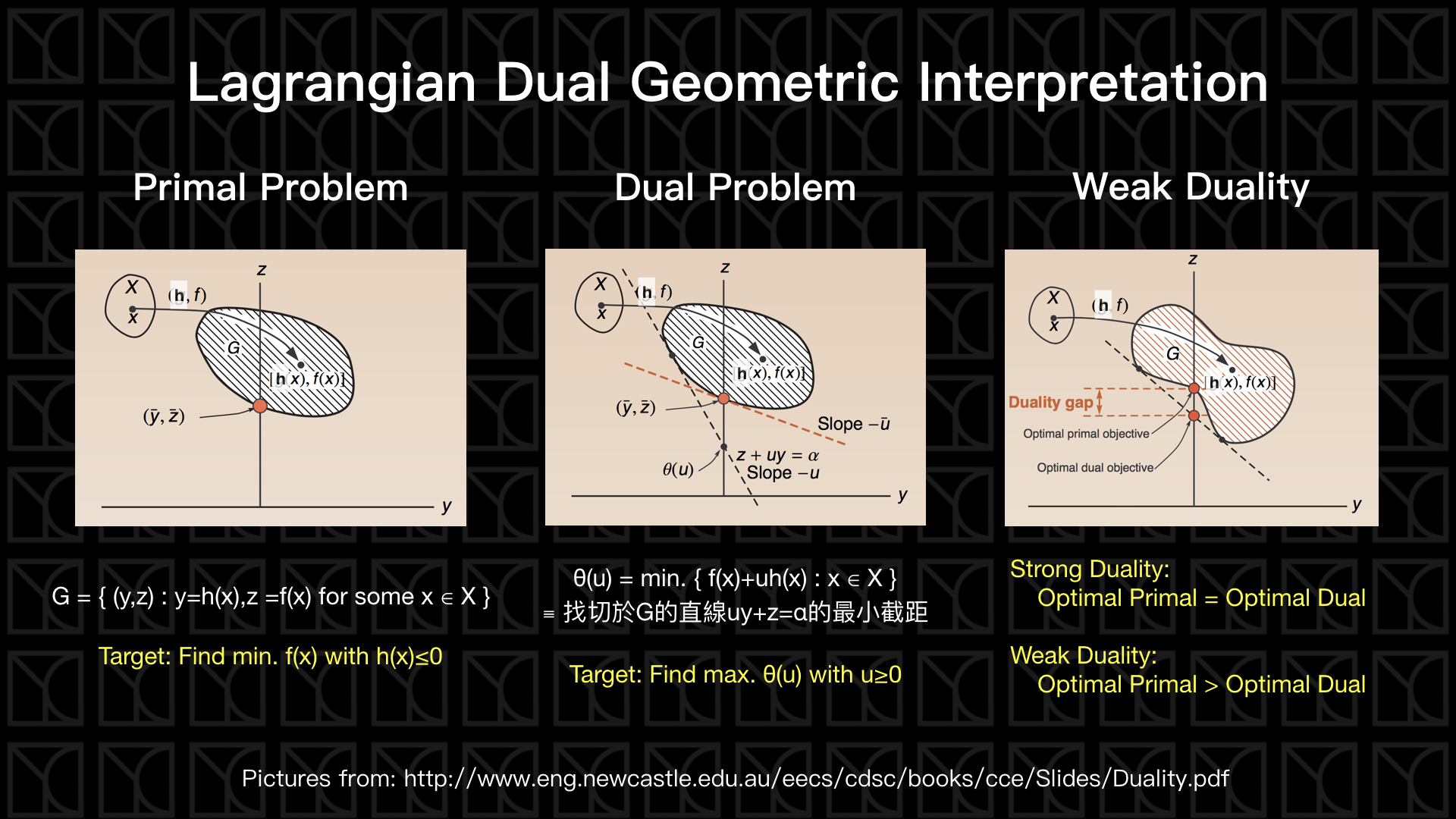
Lagrangian Dual Geometric Interpretation

我們先不管$g(x)$的部分只看$f(x)$和$h(x)$的部分，假設所有的Data $x$映射到$f(x)$和$h(x)$會產生一塊區域$G$。

在Primal Problem中我們可以很容易的找出$h_{j}(x_{1},x_{2}, … , x_{n}) ≤ 0$的限制之下$f(x_{1},x_{2}, … , x_{n})$ 的最小值，見上圖左側。

見上圖中間，Dual Problem採取另外一個方法，它先去找

$$ Θ(μ) = given\ μ\ to\ find\ min. L(x,μ),\ where: L(x,μ) = f(x)+μh(x)。 $$

$f(x)+μh(x)=α$在圖中的平面上是一條直線，而$f(x)+μh(x)$的值也就是$α$也正好是它的「截距」，所以在給定$μ$後要最小化$f(x)+μh(x)$的方法，就等效於固定直線斜率最小化截距，所以最後這個直線就必須要切於$G$才能使得截距最小，所以我們得到一條切於$G$且斜率$(-μ)$的直線，因此我們就順利的得到$Θ(μ)$的關係式了，接下來我要找出$Θ(μ)$的最大值，所以就必須往上推，這個時候你就發現答案和前面Primal Problem答案一模一樣，這種最佳化答案相同的情況稱為「Strong Duality」，而最佳化答案不相同的情況就叫做「Weak Duality」，見上圖右側，在這種$G$的形狀下，就會產生最佳化答案不相同的情況。

[進階] Hard-Margin SVM Dual + Kernel Function = Kernel Hard-Margin SVM

那我們現在可以正式的把Lagrangian Dual的東西放到Hard-Margin SVM上面。

回想一下Hard-Margin SVM的問題是：

在$y_{n}×(W^{T}X_{n}+b) ≥ 1 ,\ n=1\cdots N$的條件下，求$(W^{T}W/2)$ 最小的情形。

那如果加上非線性轉換，從$X$空間轉到$Z$空間，則問題變成

在$y_{n}×(W^{T}Z_{n}+b) ≥ 1 ,\ n=1\cdots N$的條件下，求$(W^{T}W/2)$ 最小的情形。

所以我們可以使用Lagrangian Multiplier來解決問題，依以下步驟：

假設Lagrange Function： $L(W,b,α) = (W^{T}W/2) + 𝚺_{n} α_{n} × [1-y_{n}×(W^{T}Z_{n}+b)]$
考慮Primal Feasibility、Complementary Slackness、Dual Feasibility的限制
Primal Feasibility Condition：$1-y_{n}×(W^{T}Z_{n}+b) ≤ 0$ [式1-1]
Complementary Slackness Condition：$α_{n} × [1-y_{n}×(W^{T}Z_{n}+b)] = 0$ [式1-2]
Dual Feasibility Condition：$α_{n} ≥ 0$ [式1-3]
先求出$Θ(α) = given α to find min. L(W,b,α)$
$𝞉L / 𝞉b = - 𝚺_{n} α_{n}y_{n} = 0$ [式1-4]
$𝞉L / 𝞉W_{n} = |W|- 𝚺_{n} α_{n}y_{n}Z_{n} = 0$，$y_{n}Z_{n}$應該和$W$同向，所以 $W = 𝚺_{n} α_{n}y_{n}Z_{n}$ [式1-5]
因此$L(W,b,α)$只要滿足[式1-4]和[式1-5]就代表是極小值了
所以[式1-4]和[式1-5]代入得$Θ(α,β) = (-1/2)𝚺_{n}𝚺_{m} α_{n}α_{m}y_{n}y_{m}Z_{n}Z_{m}+𝚺_{n} α_{n}$
求$Θ(α)$極大值
$max.[Θ(α)]＝min.[-Θ(α)]=min.[(1/2)𝚺_{n}𝚺_{m} α_{n}α_{m}y_{n}y_{m}Z_{n}Z_{m}-𝚺_{n} α_{n}]$ —[式1-6]
綜合上述[式1-3]、[式1-4]、[式1-6]並改寫成Kernel的形式得，$min. [(1/2)𝚺_{n}𝚺_{m} α_{n}α_{m}y_{n}y_{m}K(X_{n},X_{m})-𝚺_{n} α_{n}], s.t. α_{n} ≥ 0 ; \ 𝚺_{n} α_{n}y_{n} = 0$，使用QP Solver可以求出 $α_{n}$。
可以用$α_{n}$來求$W$和$b$
$α_{n}$涵義：觀察[式1-2]可得 (1) $α_{n} = 0$ 為Non-Support Vector； (2) $α_{n} > 0$ 代表$y_{n}×(W^{T}Z_{n}+b)=1$，為Support Vector。
由[式1-5]得，$W = 𝚺_{n} α_{n}y_{n}Z_{n}$，從式子中你會發現對W有貢獻的只有Support Vector $(α_{n}>0)$。
假設在某個Support Vector($α_{n}>0$)上，由[式1-2]可推得，$b=y_{sv}-𝚺_{n} α_{n}y_{n}K(X_{n},X_{sv})$ (at Support Vector)。

[進階] Soft-Margin SVM Dual + Kernel Function = Kernel Soft-Margin SVM

考慮Soft-Margin SVM和特徵轉換：

在$y_{n}×(W^{T}Z_{n}+b) ≥ 1-ξ_{n}$且$ξ_{n} ≥ 0,\ n=1\cdots N$的條件下，求$(W^{T}W/2) + C 𝚺_{n} ξ_{n}$最小的情形。

所以我們可以使用Lagrangian Dual Problem來解決問題，依以下步驟：

假設Lagrange Function： $L(W,b,ξ,α,β) = (W^{T}W/2) + C 𝚺_{n} ξ_{n} + 𝚺_{n} α_{n} × [1-ξ_{n}-y_{n}×(W^{T}Z_{n}+b)] + 𝚺_{n} β_{n} × [-ξ_{n}]$
考慮Primal Feasibility、Complementary Slackness、Dual Feasibility的限制
Primal Feasibility Condition：$1-ξ_{n}-y_{n}×(W^{T}Z_{n}+b) ≤ 0$ [式2-1]；$-ξ_{n} ≤ 0$ [式2-2]
Complementary Slackness Condition：$α_{n} × [1-ξ_{n}-y_{n}×(W^{T}Z_{n}+b)] = 0$ [式2-3]；$β_{n} × [-ξ_{n}] = 0$ [式2-4]
Dual Feasibility Condition：$α_{n} ≥ 0$ [式2-5]；$β_{n} ≥ 0$ [式2-6]
先求出$Θ(α,β) = given\ α,β\ to\ find\ min. L(W,b,ξ,α,β)$
$𝞉L / 𝞉b = - 𝚺_{n} α_{n}y_{n} = 0$ [式2-7]
$𝞉L / 𝞉W_{n} = |W|- 𝚺_{n} α_{n}y_{n}Z_{n} = 0$，$y_{n}Z_{n}$應該和$W$同向，所以 $W = 𝚺_{n} α_{n}y_{n}Z_{n}$ [式2-8]
$𝞉L / 𝞉ξ_{n} = C - α_{n} - β_{n} = 0$ [式2-9]
因此$L(W,b,ξ,α,β)$只要滿足[式2-7]、[式2-8]和[式2-9]就代表是極小值了
所以[式2-7]、[式2-8]和[式2-9]代入得$Θ(α,β) = (-1/2)𝚺_{n}𝚺_{m} α_{n}α_{m}y_{n}y_{m}Z_{n}Z_{m}+𝚺_{n} α_{n}$
求$Θ(α,β)$極大值
$max.[Θ(α,β)]＝min.[-Θ(α,β)]=min.[(1/2)𝚺_{n}𝚺_{m} α_{n}α_{m}y_{n}y_{m}Z_{n}Z_{m}-𝚺_{n} α_{n}]$ —[式2-10]
綜合上述[式2-5]、[式2-6]、[式2-9]、[式2-10]並改寫成Kernel的形式得，$min. [(1/2)𝚺_{n}𝚺_{m} α_{n}α_{m}y_{n}y_{m}K(X_{n},X_{m})-𝚺_{n} α_{n}],\ s.t. 0 ≤ α_{n} ≤ C;\ 𝚺_{n} α_{n}y_{n} = 0$，使用QP Solver可以求出 $α_{n}$。
可以用$α_{n}$來求$W$和$b$
$α_{n}$涵義：觀察[式2-3]和[式2-4]可得 (1) $α_{n} = 0$ 為Non-Support Vector； (2) $0 < α_{n} < C$ 代表$y_{n}×(W^{T}Z_{n}+b)=1$，為Free Support Vector；(3) $α_{n} = C$ 代表$y_{n}×(W^{T}Z_{n}+b)=1-ξ_{n}$，為Bounded Support Vector。
由[式2-8]得，$W = 𝚺_{n} α_{n}y_{n}Z_{n}$，從式子中你會發現對W有貢獻的只有Support Vector ($α_{n}>0$)。
假設在某個Support Vector($α_{n}>0$且$β_{n}>0$)上，由[式2-3]和[式2-4]可推得，$b=y_{sv}-𝚺_{n} α_{n}y_{n}K(X_{n},X_{sv})$ (at Support Vector)。

Previous Post Next Post