機器學習基石 學習筆記 (4):機器可以怎麼學得更好?
Posted on September 18, 2016 in AI.ML. View: 17,991
前言
在上一回中,我們已經了解了機器學習基本的操作該怎麼做。而這一篇中,我們來看機器可以怎麼學得更好? 基本上有三招:Feature Transformation(特徵轉換)、Regularization(正規化)和Validation(驗證),我們來看看。
Feature Transformation(特徵轉換)

在上一回當中我們講了很多的線性模型,大家有沒有懷疑說,數據呈現的方式一定可以用線性描述嗎?我的答案是通常線性描述會表現不錯,但不是絕對,那我們怎麼用非線性的方法來描述我們的數據,這邊提供一個方法叫做「非線性轉換」,或者又稱為「特徵轉換」(還記得變數\(x\)又可以稱為特徵Features),聽起來有點困難齁~其實不會啦!
假設今天你的Data分布是圓圈狀的分布,顯而易見的你很難用一條線去區分他們,那我們應該怎麼做呢?假設今天有一個轉換可以把這個圓圈狀分布的空間轉換到另外一個空間,而且在這個新的空間,我們可以做到線性可分,這樣問題就解決了,我們非常擅長做線性可分啊!怎麼做呢?我們知道這個空間分布是圓圈分布,所以套用以前學過的公式:
,如此一來,令 \(z_1=-x_1^2\); \(z_2=-x_2^2\),所以問題就變成一個線性問題
在做這個操作時,我們會用到非線性項,也就是高次項或交叉項,所以會稱這個轉換叫做「非線性轉換」。藉由人為觀察數據,並給予適當的特徵轉換,找出其中隱藏的非線性項當作新的特徵,又稱為特徵工程(Feature Engineering)。
但如果我們需要去人為定義這個「非線性轉換」,這就很弱啦!我們當然希望機器可以自行從Data中學習到這個轉換,作法是這樣的,我們先把變數\(x\)做個變化和擴充,讓它們互相的相乘創造出高次項,再把這些項等價的放到Linear Model裡,所以我們就用了線性的作法來做到Non-linear Model,而因為有權重\(W\)在非線性項前面的關係,所以機器會針對Data自行去調配非線性項或線性項的權重\(W\),這效果就等同於機器自行學習到「非線性轉換」。
機器自己學習特徵轉換的這個概念應該是現今ML最重要的概念之一,最近很夯的深度學習就擁有強大的特徵轉換功能,這些轉換都是機器從Data自行學來的。
特徵轉換讓ML變得很強大,但要特別注意,因為我們增加了非線性項,所以等於是增加了模型的複雜度,這麼做的確可以壓低\(E_{in}\)沒有錯,但也可能使得\(E_{in} \approx E_{out}\)不再成立,也就是Overfitting,所以建議要逐步的增加非線性項,從低次方的項開始加起,避免Overfitting。
Overfitting
Overfitting是一個大怪獸,在學習怎麼對付牠之前,我們先來好好的了解牠!
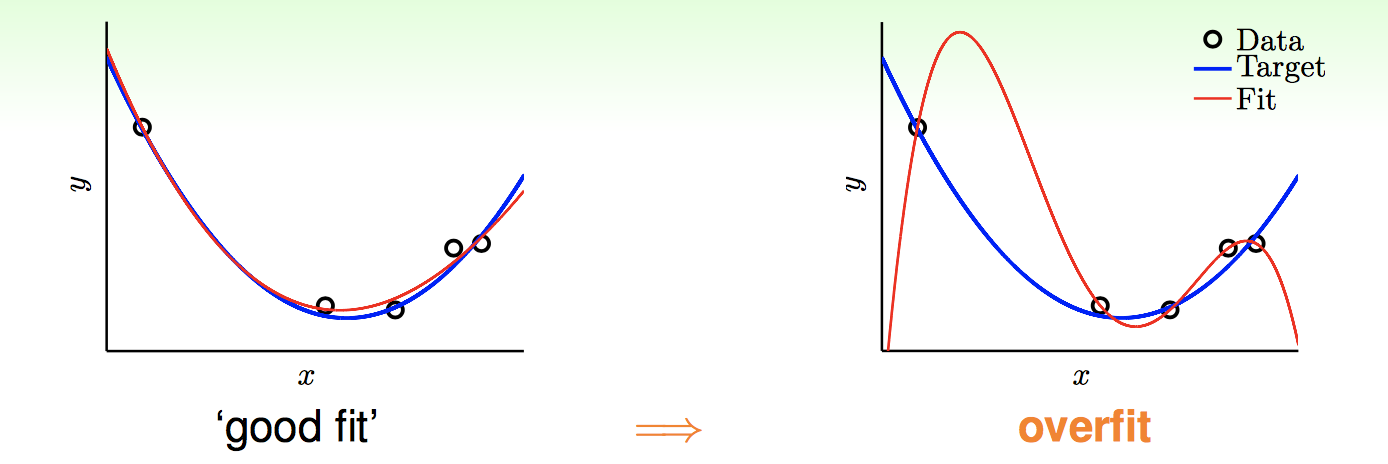
From: https://www.csie.ntu.edu.tw/~htlin/course/mlfound17fall/doc/13_handout.pdf
上面這張圖用很簡單的方法說明了Overfitting是怎麼一回事,假設藍色的線是Target,也就是我們抽樣的母群體,因為雜訊的關係,抽樣出來的點可能會稍微偏離Target,而如果這個時候我們用二次式來描述這些抽樣出來的Data(上圖中的左側)會發現\(E_{in}\)不能壓到0,所以這個時候可能有人想說加進去更高次項來試試看(上圖中的右側),此時會發現\(E_{in}=0\),所有數據都可以被完整描述了,但是你會發現Fit的曲線已經完全偏離了Target,反而是使用低次項還描述比較好,低次項描述的\(E_{in}\)和 \(E_{out}\)(Target Function) 比較接近,所以結論是如果我們把「隨機雜訊」(Stochastic Noise)Fit進去Model裡面就會因此產生Overfitting,要避免這種情況發生,就要小心使用高次項。
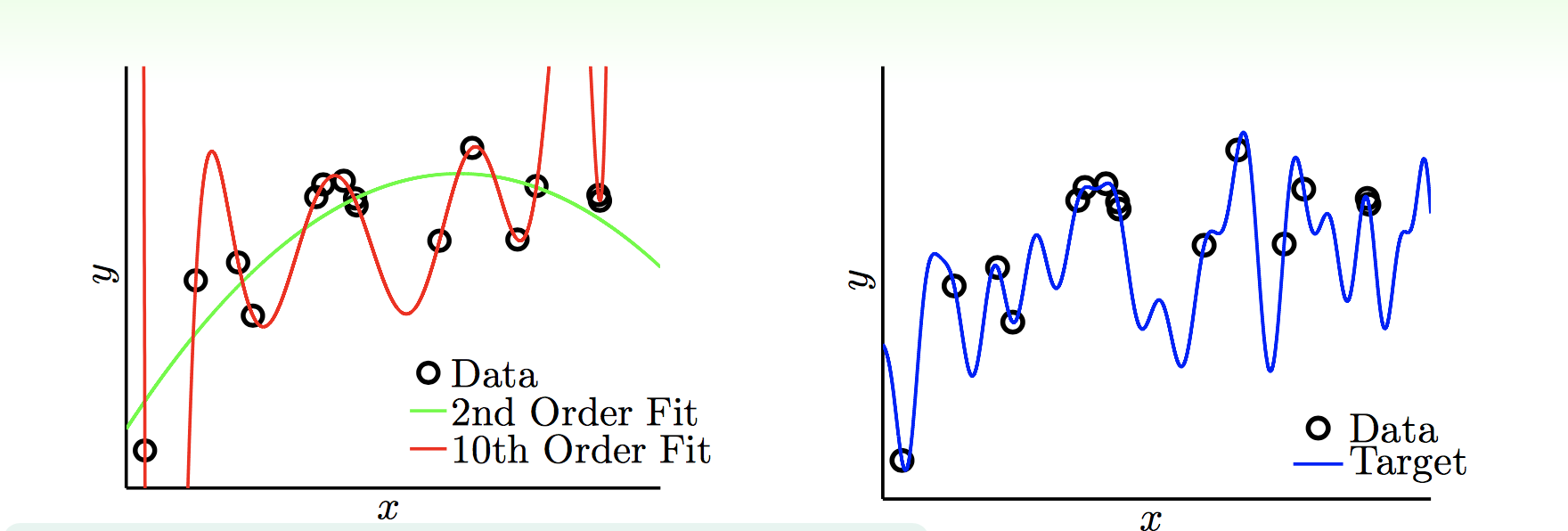
From: https://www.csie.ntu.edu.tw/~htlin/course/mlfound17fall/doc/13_handout.pdf
但可別以為沒有「隨機雜訊」鬧場就不會出現Overfitting,上圖假設一個沒有「隨機雜訊」的情形,但是這次Target Function的複雜度很高(上圖右側),當我們從中採樣一些Data來進行Fitting,如上圖左側,我們分別使用2次和10次來做Fitting,這個時候你會發現雖然2次和10次都和Target曲線差很遠,但是小次方的還是Fit的比較好一點,造成Overfitting的原因是因為當Target很複雜的情況下,如果採樣的數據不大,根本無法反應Target本身,所以就算使用了和Target一樣複雜的Model,也只是在瞎猜而已。這種因為Target本身的複雜度所帶來的雜訊,我們稱為「決定性雜訊」(Deterministic Noise)。
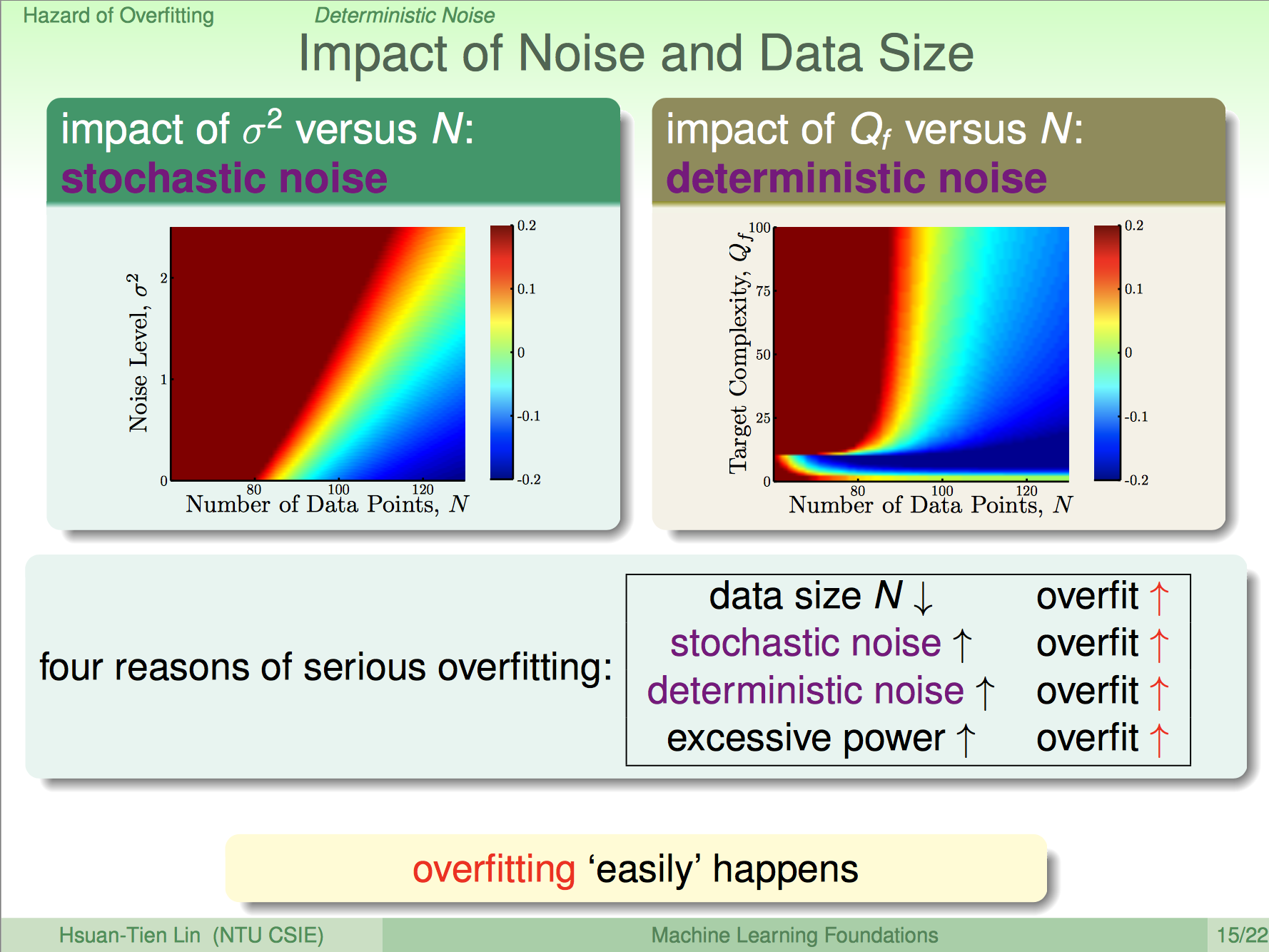
From: https://www.csie.ntu.edu.tw/~htlin/course/mlfound17fall/doc/13_handout.pdf
我們來看一下「隨機雜訊」(Stochastic Noise)和「決定性雜訊」(Deterministic Noise)怎麼造成Overfitting的,上圖中的兩張漸層圖表示的是Overfitting的程度,越接近紅色代表Overfitting越嚴重;反之,越接近藍色則Overfitting越輕微。左邊的漸層圖是考慮「隨機誤差」的影響,右邊的漸層圖則是考慮「決定性雜訊」的影響。從這兩張圖我們可以觀察出下面四點特性:
- Data數量\(N\)越少,越容易Overfitting
- 「隨機雜訊」越多,越容易Overfitting
- 「決定性雜訊」越多,越容易Overfitting
- Model本身越複雜,越容易Overfitting
那有什麼方法可以防止Overfitting嗎?有的,包括之前講過的一些方法,我們來看一下:
- 從簡單的模型開始做起,從低次模型開始做起,在慢慢加入高次項
- 提升資料的正確性:Data Cleaning/Pruning(資料清洗)將錯誤的Data修正或刪除
- Data Hinting(製造資料),使用合理的方法擴增原有的資料,例如:在圖形辨識問題中,可以用平移和旋轉來擴增出更多Data
- Regularization(正規化):限制權重W的大小以控制高次的影響。(接下來會詳述...)
- Validation(驗證):將部分Data保留不進去Fitting,然後用這個Validation Data來檢驗Overfitting的程度。(接下來會詳述...)
Regularization(正規化)
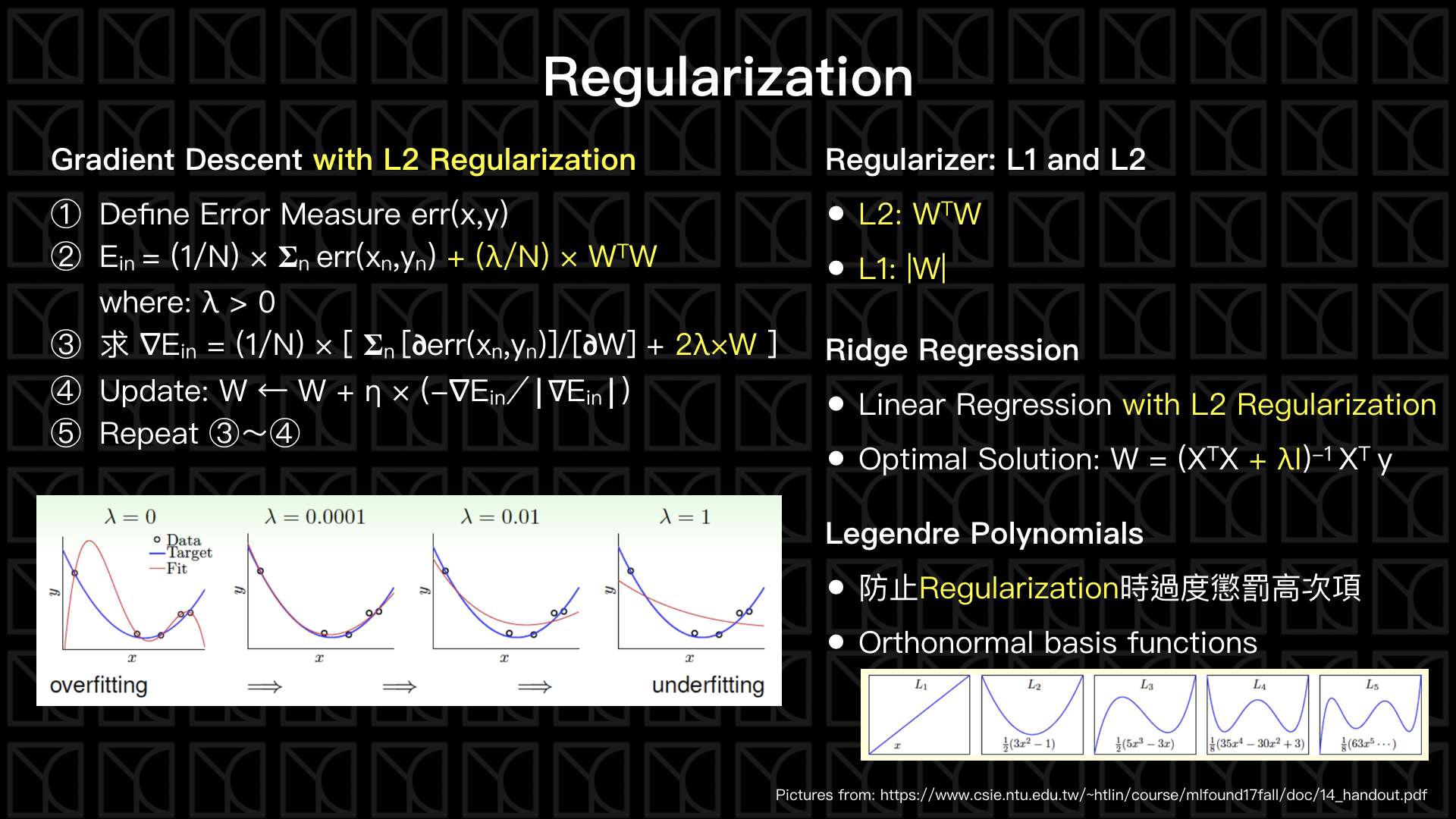
剛剛我們提到了Overfitting所造成的影響很大一部分是因為Model複雜度所造成的,但是為了可以把\(E_{in}\)給壓下去,我們又的確需要去增加高次項,所以依照建議需要從低次項開始慢慢的加,這樣感覺很麻煩啊!有沒有辦法讓機器自己去限制高次項的出現呢?有的,這就是Regularization(正規化)。
還記得剛剛在講「特徵轉換」時,有提到一點,ML有辦法自行學習「特徵轉換」的關鍵是因為高次項前面有一個可調控的權重,而機器會針對Data來調整權重大小,那其實就是等價於機器自己學習到了「特徵轉換」,同理可知,我們只要限制權重\(W\)的大小就等同於限制了機器無所忌憚的使用高次項。
經數學證明,限制權重\(W\)的大小可以等價於在\(E_{in}\)上面加上「\(W\)大小的平方」乘上定值\(λ\),\(λ\)越大代表\(W\)大小限制越緊;\(λ\)越小代表\(W\)大小限制越鬆,這也非常容易想像,訓練Model的方法是去降低\(E_{in}\),但是如果使用了大的\(W\),就會使得\(E_{in}\)增大,自然而然在訓練的過程中,機器會去尋找小一點的\(W\),也就等同於限制了\(W\)的大小。
見上圖左側,我們修改了Gradient Descent讓它受到Regularization的限制。
而上圖左側下方,顯示了在\(λ\)增大的同時,限制\(W\)的大小會越來越緊,所以Fitting的結果從原本的Overfitting變成Underfitting。
Underfitting所代表的是Model本身的複雜度不夠,不足以使得\(E_{in}\)降的夠小,如果你經過Validation(待會會講)後發現沒有Overfitting的現象,但是你的\(E_{in}\)始終壓不下來,那就有可能是Underfitting,那你該考慮的是增加Model複雜度或者放寬Regularization,反而不是Regularization。
Regularizer的選擇常見的有兩種L2和L1,L2使用「\(W\)大小的平方」,L1則使用「\(W\)大小的絕對值」。
當Linear Regression使用Regularization限制,統計上有一個名稱稱為Ridge Regression,你可以使用Gradient Descent來做,又或者使用解析解的方法。
最後提一個Regularization的細節,你會發現因為高次項是彼此兩兩相乘的結果,所以項目的個數會隨著次方增加而增加,這麼一來在做Regularization時可能會過度懲罰高次項,因此,我們可以將Feature轉換成Legendre Polynomials來避免這個問題。
Validation(驗證)
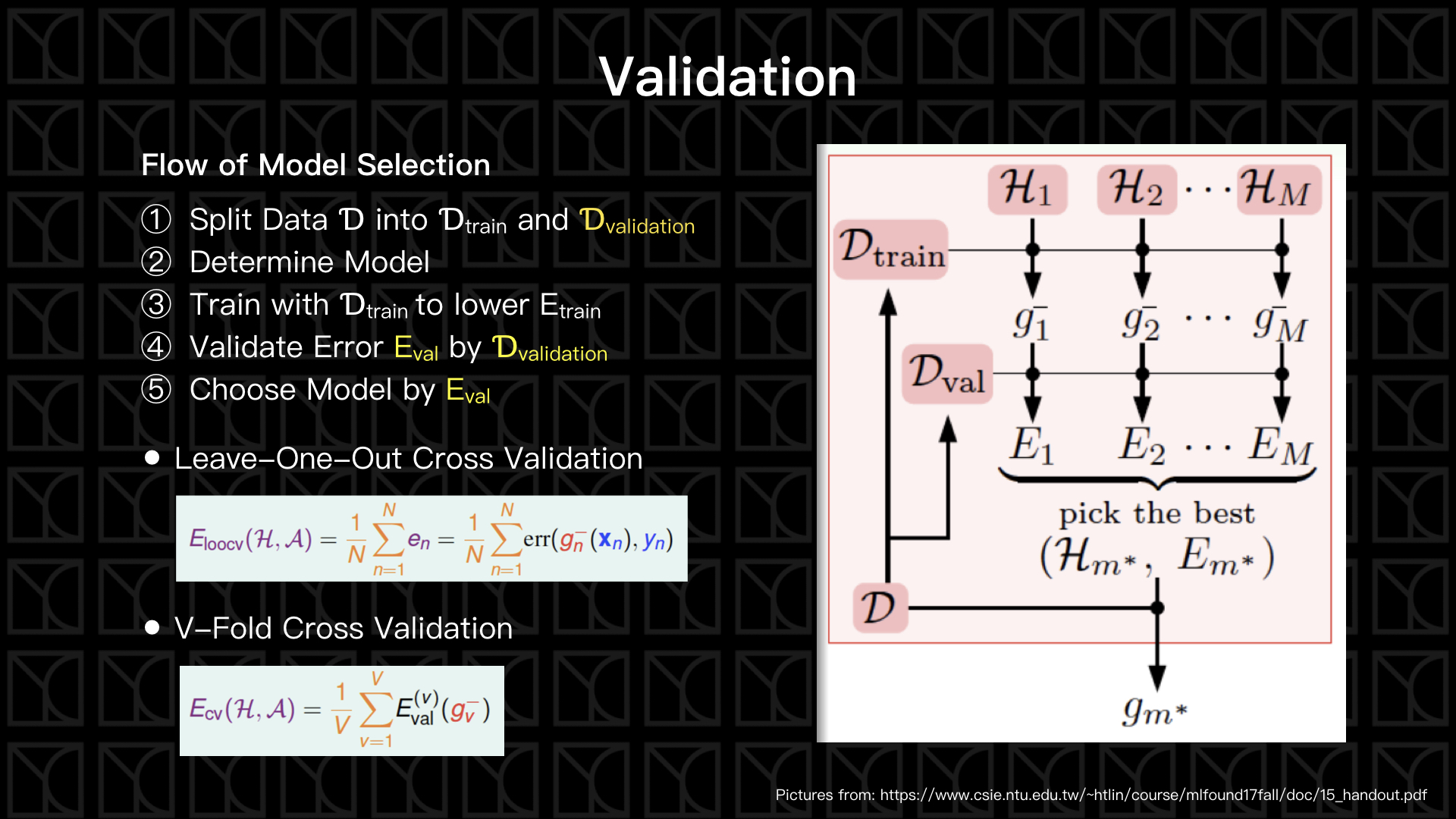
講了這麼多Overfitting,但到底要怎麼去量化Overfitting呢?Overfitting就是\(E_{in} \approx E_{out}\)不成立,但是\(E_{out}\)我們不會知道啊!因為我們不會知道Target Function是什麼,那該怎麼得到量化Overfitting的值呢?
有一個方法叫做Validation可以拿來量化Overfitting的值,這個方法是先將採樣的數據做分離,一部分將會拿來做Model Fitting(Model Training),另外一部分保留起來評估訓練完畢的Model,因為保留的這一部分源自於母群體,而且又沒有被Model給看過,所以它可以很客觀的反應出\(E_{out}\)的大小。
我們的Model和Algorithm從以前講到現在已經是越來越複雜了,來複習一下Model和Algorithm受哪些參數影響,Algorithm的選擇就有很多了,包括:PLA、Linear Regression、Logistic Regression;Learning Rate \(η\)也需要去選擇大小決定學習速率;Feature Transformation中Feature的決定和次方大小的決定;Regularization也有L2、L1 Regularizer的選擇;還有Regularization的\(λ\)值也必須被決定。
這些條件彼此交互搭配會產生很多組的Model,那該如何挑選Model呢?我們就可以使用Validation來當作一個依據來選擇Model,選擇出\(E_{val}\)最小的Model,如上圖所示。
另外實作上有一些方法:Leave-One-Out Cross Validation和V-Fold Cross Validation,他們的精髓就是保留\(k\)筆Data當作未來Validation用,另外一些拿下去Train Model,然後再用這k筆去評估並得到\(E_{val,1}\),還沒結束,為了讓\(E_{val}\)盡可能的正確,所以我們會在把Data作一個迴轉,這次使用另外一組k組Data來Validation,其餘的再拿去Train Model,然後在評估出,\(E_{val,2}\) … 以此類推,當轉完一輪之後,在把這些\(E_{val,1}\), \(E_{val,2}\), ...做平均得到一個較為精確\(E_{val}\)。那Leave-One-Out Cross Validation顧名思義就是\(k=1\),但這樣做要付出的代價就是計算量太大了,所以V-Fold Cross Validation則使用\(k=V\)來做。實務上,我常常做Validation時根本不會去Cross它們,我大都只是保留一部分的Data來驗證而已,給大家參考。
總結
來到了這四篇有關於林軒田教授機器學習基石學習筆記的尾聲了,讓我們重溫看看我們學會了什麼?
一開始我帶大家初探ML的基本架構,建立Model、使用Data訓練、最後達到描述Target Function的目的,也帶大家認識各種機器學習的類型。
接下來,我們用理論告訴大家,ML是不是真的可以做到,那在什麼時候可以做到?要符合哪些條件?我們知道要有好的Model,VC Dimension越小越好,也就是可調控的參數越少越好,才會使得\(E_{in} \approx E_{out}\)成立;要有足夠的Data;要有好的Learning Algorithm能把\(E_{in}\)壓低,這三種條件成立後,如此一來Model在描述訓練數據很好的同時也可以很好的去預測母群體,但我們發現\(E_{in}\)壓低和可調控的參數越少越好兩者是Trade-off,所以我們必須取適當的VC Dimension。
再接下來我們開始看實際上ML該怎麼做,引入相當重要的Learning Algorithm,也就是Gradient Descent,並且說明了Linear Regression和Logistic Regression,而且還可以使用這兩種Regression來做分類問題。
那最後就真正亮出ML的三大絕招啦:Feature Transformation(特徵轉換)、Regularization(正規化)和Validation(驗證),Feature Transformation使得Model更為強大,所以\(E_{in}\)更能夠壓低,但是為了避免Overfitting我們必須去限制它,Regularization可以限制高次項的貢獻,另外,Validation可以量化Overfitting的程度,有了這個我們就可以去選出體質健康而且\(E_{in}\)又小的Model。
機器學習基石的這些概念都很重要,往後如果你開始學習其他的ML技巧,例如:深度學習,這些知識都是你強大的基礎,所以多看幾次吧!