機器學習基石 學習筆記 (1):何時可以使用機器學習?
Posted on June 06, 2016 in AI.ML. View: 14,200
前言
經過幾個月的努力,終於完成田神在Coursera上machine learning的兩門課中的第一門課—機器學習基石,田神不愧為田神的名號,整門課上起來非常流暢,每個觀念講得非常得清晰,考究學理,但是又不會單單只有理論而已,課程中會舉很多實用的例子,讓你了解每個觀念如何實踐。因此,非常推薦大家去把Coursera上面的課程完整聽一次,應該會收益良多,接下來一系列的文章,我會摘要出《機器學習基石》之中主要的概念,適合對Machine Learning(ML)有興趣的初學者來一窺它的脈絡。
《機器學習基石》一共有16堂課,主要分為四個方向,第一個方向,何時可以使用機器學習(When Can Machines Learn? ),點出什麼是機器學習,適合在哪些情形下使用,並引入貫穿整個課程的二元分類問題,第二個方向,為什麼機器可以學習(Why Can Machines Learn?),介紹學理上機器學習必須要有哪些條件才可行,這些理論是了解機器學習非常重要的內功,第三個方向,機器可以怎麼樣學習(How Can Machines Learn?),學習完了學理,我們來看機器學習有哪些的使用方法,最後一個方向,機器可以怎麼樣學得更好(How Can Machines Learn Better?),探討哪些問題會造成機器學不好,然後怎麼去改善。
什麼是Machine Learning (ML)
在了解機器學習之前,我們不妨來想想「你」從小是怎麼學習的,有人會說學習就是一個不斷記憶的過程,但這樣的說法顯然不夠全面,你總不會認為把考題的所有答案都背起來的學生就已經學會一門知識了吧!所以,考題只是表象,我們真正要學習的是它背後的觀念,可以拿來推敲未知的知識。
同樣的,ML的學習方式也有點類似於人類的學習,機器從Data中開始學習起,這些Data就像是一道一道的考題,而ML做的事正是去學習Data後面的觀念,而不是單純把Data給儲存起來,有了Data背後的觀念才能舉一反三,才算是真正的學會了。
所以,做ML有點像是手把手的造一顆大腦,並且訓練它學會Data背後的知識。那這個大腦要怎麼設計呢?這個大腦用我們學物理的人的說法就是建一個Model,而餵給它Data的過程就是Model Fitting。
那什麼是Model呢?讓我來解釋一下,所謂的Model就是給一個未知現象的框架來試圖描述它,舉個例子,我們都知道力的公式是\(F=ma\)(力=質量x加速度),但如果你今天拿一顆皮球來,你就會發現這個公式並不那麼正確,因為皮球會形變,那怎麼辦呢?我們可以假設形變會把部份的力給抵消掉,所以式子改寫成\((F-F_1)=ma\),在這邊\(F_1\)就是那個抵消的力,這樣就是設計了一個Model來描述這個現象,而\(F_1\)是一個未知的值,我們可以用實驗數據來推估\(F_1\),這就是所謂的Model Fitting。
物理上的Model通常是這樣做的,我們先觀察未知現象,然後從中猜測可能造成這現象的原因,總結這些原因來設計一個Model,Model中可能有一些參數還沒被決定,此時我們就可以用數據來決定它,這就是Model Fitting。
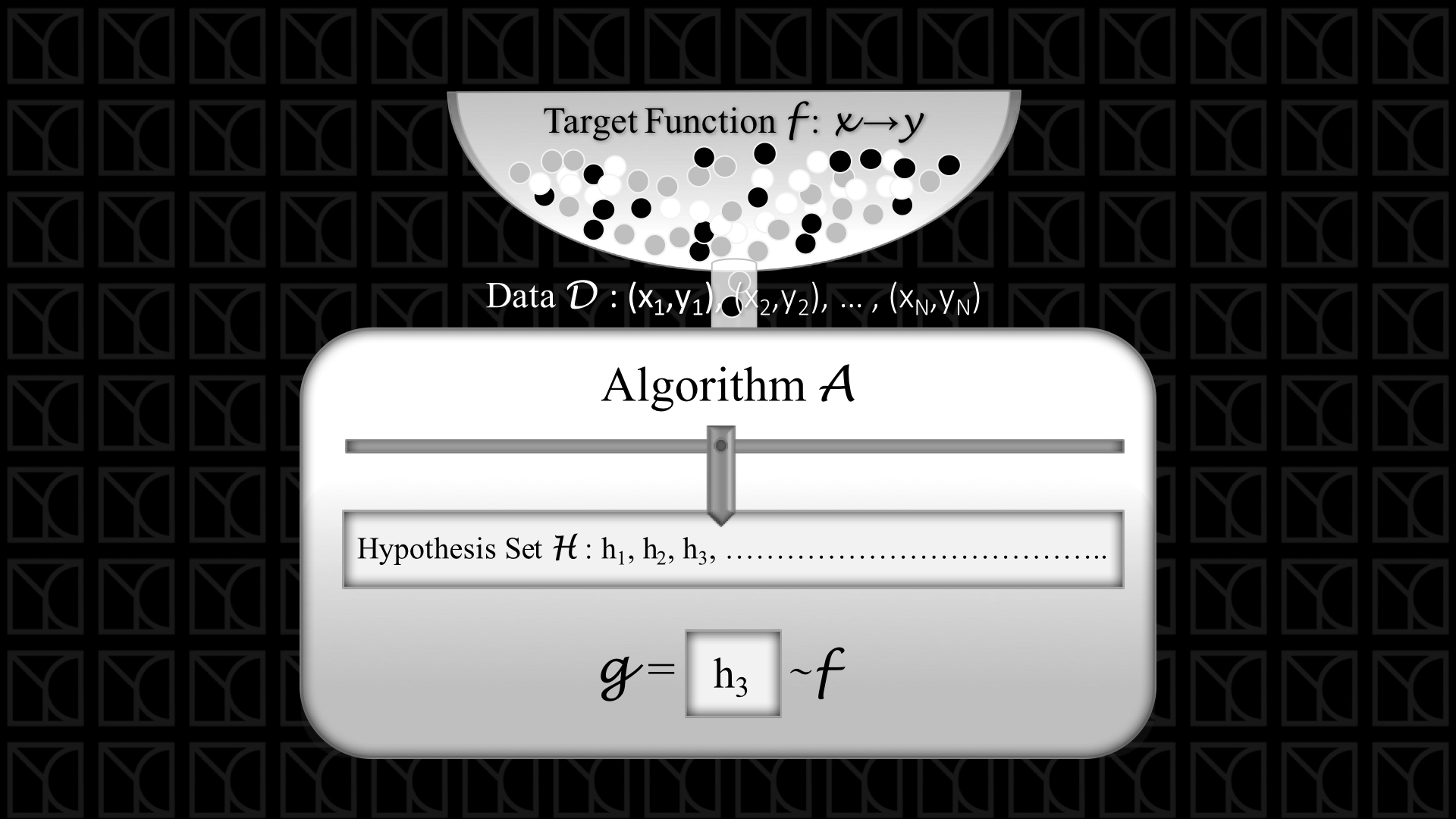
了解了Model的概念就相當好了解ML的架構,上圖是ML的基本架構,假設我們今天要讓機器學一樣技術,這個技術我們用一個函數來表示,稱之為Target Function,這個Target Function就是隱藏在Data後面的真正道理,每個變數\(X\)會有相應的正確答案\(Y\)。
今天我從Target Function中取出\(N\)組當作Data來給我的機器學習,那目標是什麼?目標當然是讓機器學習出這個Target Function啦!所以我們要先設計我們的Model,最終目的是決定Model裡的參數之後,這個被選擇的Model就是Target Function。
Model就是上圖中的Hypothesis Set,在Model參數還沒被決定之前,你可以想像它就像一個集合包含很多可以選擇的函數,而使用數據Model Fitting以後,選出一組最佳化的參數,就好像從這個集合中挑選一組函數一樣。
在這個找最佳化參數的過程,我們需要一個機制,這個機制可以評估Hypothesis Set中每組函數描述Data的好壞,並且找出描述Data最好的那組參數,這個機制就是上圖中的Learning Algorithm。
建立Model,使用Data加上Learning Algorithm找出最佳參數,這就是ML的架構輪廓。當然這邊要補充一下,物理上的Model通常是建基在已知的知識之上,而常見的ML強大之處是不需要太多的人為的智慧,機器可以自行學習,所以我這裡指的Model是比物理上的Model更加廣義的。
Machine Learning (ML)的使用時機
剛剛帶大家初探了ML的架構,接下來帶大家了解什麼時候我們適合使用ML。
舉幾個例子,大家可能比較有感覺,譬如說Netflix曾辦過一場競賽,競賽的內容是利用客戶的影片評分紀錄,來預測未評分影片的得分,如果可以增進預測率10%,就可以獨得100萬美元獎金,這個問題就可以使用ML,Data是過去得評分紀錄,Target Function是用戶評分的規律,如此一來,機器學到了這個技術,未來就可以舉一反三的推出未評分影片的分數,和用戶喜歡的影片可能有哪些。
再多看幾個例子,例如設計火星勘查機,人類目前對火星的了解仍相當有限,所以我們沒辦法完全猜測勘查機在火星會遇到什麼問題,所以必須讓勘查機有ML的能力去學習各種問題的解決方法。
再來個例子,現在很夯的汽車自動駕駛也需要ML技術,機器去學習辨識交通號誌。
看了這麼多例子,我們會發現這些例子都很難以寫出簡單的規則,但是卻又存在著一種規律,這種情形正是適合用ML來做。
在以往電腦工程幾乎都是由工程師用嚴謹的邏輯去逐條的把規則一一的寫上,這樣的機器不具有學習能力,或稱得上人工智慧,因為它只是單純反應工程師的工人智慧而已,但如果遇到一些困難的問題,譬如告訴機器什麼是狗,這時候你就會發現很難用人為規則來描述它,有尾巴,可是是怎樣的尾巴?有耳朵,那這耳朵怎麼和貓的耳朵區分開來?此時要用人為寫出規則就太困難了,我們不這麼做,反過來我們設計架構讓機器自己去從Data中學習。
總結一下上面的重點,ML的最佳使用時機包含下面三種情形
- 你想要學習的技術存在一種模式
- 要學習的技術不容易簡單的列出規則
- 存在可以代表這個要學習的模式的Data
二元分類問題
from: https://class.coursera.org/ntumlone-003/lecture/17
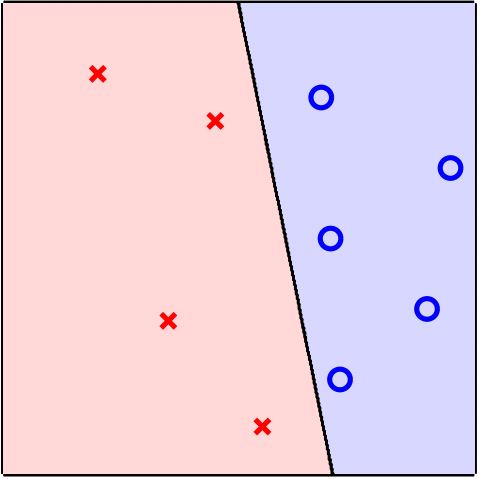
好! 大家現在應該對於機器學習有一些認識了,那接下來我們來實作一些例子來了解機器學習架構怎麼運作。像個小學生一樣,我們先從簡單的是非題來學起,是非題學究一點的講法就是「二元分類問題」。
舉個例子,今天有一家銀行想要開發一款ML的軟體,這個軟體可以根據過去信用卡核發用戶的資料,去判斷要不要核發信用卡給這個新的申請人,這些過去的資料可能包括:用戶年齡、用戶性別、用戶年薪等等,讓機器藉由這些資料去學習判斷要不要核發信用卡。把這樣的二元分類問題化作
Target Function:\(f: X → y\)
\(X\)有年齡、性別和年薪這些變數,而\(y\)則是個二元類別,不是\(y=1\)(核發)就是\(y= -1\)(不核發)。
那接下來,我們就要決定我們的Learning Model,也就是Hypothesis Set。

引入Perceptron(感知器) Hypothesis Set來當作我們的Hypothesis Set,如上圖,我們給予我們的輸入變數個別的權重,然後相加起來,並且看這個值是正還是負,來決定輸出值是\(+1\)或\(-1\),\(sign\)函數的作用是假設輸入的值為正則輸出\(+1\),反之則輸出\(-1\)。
對應核發信用卡這個例子,
\(x_1\) = 用戶年齡; \(x_2\) = 用戶性別; \(x_3\) = 用戶年薪,
在分別乘上weight \(w_1\), \(w_2\), \(w_3\),這個變數前面的weight代表這個變數對於答案\(Y\)有什麼影響,如果是正向影響,\(weight > 0\),如果沒有影響,\(weight = 0\),如果負向影響,\(weight < 0\),舉個例子,高年薪也許可以提升核發信用卡的機會,那它前面的weight應該就是正的,也許性別並不影響核發信用卡的機會,則\(weight = 0\),那麼考慮到這些input變數對結果影響的評估,我們會得到一個數值 \((w_1\times x_1+w_2\times x_2+...)\)。
此時我們要用這個數值去做「二元分類」,也就是一分為二,怎麼做呢? 很簡單,給他一分水嶺,高於一個閥值我就給他 \(y=+1\),低於一個閥值我就給他\(y=-1\),假設這個閥值為\((-w_0)\),則分類依據就可以表示為 \(sign(w_0+w_1\times x_1+w_2\times x_2+...)\) 。
上圖中的 \(s = w_0+w_1\times x_1+w_2\times x_2+...\) 就像一個分數(score)一樣,高分 \(s>0\) 的我就核發(\(+1\)),低分 \(s < 0\) 的我就不核發(\(-1\)),其中權重 \(w_0, w_1, w_2, ...\) 都可以由機器學習去調整,這些不同的weight就構成了Hypothesis Set,也就是Model,那接下來我們還需要Learning Algorithm來取出最佳參數,也就是決定一組最佳weight來選出最吻合數據的Hypothesis。

如上圖所示,Perceptron Learning Algorithm(PLA)是用於處理Perceptron Hypothesis Set的一種演算法。
它的作法簡單來講是,藉由一筆一筆的數據去逐步的更新它的weight使得Model可以描述這筆數據,直到不需要再更新為止,此時所有的Data都可以用這個Model表示,更新的方法是先判斷進來的這筆數據是否符合目前的Model預測,如果不符合,此時\(\left[...\right]\)為\(+ 1\),則必須朝變數向量\(X_n\)的方向,前進或後退大小為Learning Rate的一步來更新weight,前進還是後退端看你的Data是\(y=-1\)或\(+1\),\(y=+1\)就往前進,\(y=-1\)就往後退。
因此,這個跨步更新的動作必須可以使Model接近正確答案,這麼神奇,真的假的?不太直覺,先從score來想起,假設有一筆資料為\((X_n,y_n)\),則Score:\(s = W_t・X_n\),在\(W_t\)和\(X_n\)向量彼此有同向分量的情況下,\(s > 0\),如果這個時候\(y_n\)剛好為\(+1\),則\(sign(s)=y_n\),這個時候\(W_t\)描述這個數據就很好啊,我們就不需要去更新它;如果相反\(y_n=-1\),這個\(W_t\)描述這個數據就不正確,也就是說\(W_t\) 和 \(X_n\)不應該同向,所以我們讓\(W_t\)加上\(-X_n\)(\(=y_n\times X_n\)),把\(W_t\)從原本與\(X_n\)同向的狀態反向拉離開來。那如果在\(W_t\)和\(X_n\)向量彼此不同向的情況下,\(s < 0\),這個時候如果\(y_n\)剛好為\(-1\),則\(sign(s)=y_n\),很好我們不去更新它;如果相反\(y_n=+1\),這個\(W_t\)描述這個數據不正確,也就是說\(W_t\) 和 \(X_n\)不應該反向,所以我們讓\(W_t\)加上\(X_n\)(\(=y_n\times X_n\)),把\(W_t\)拉到和\(X_n\)同向一點。這就是PLA找到更好\(W_t\)的機制。
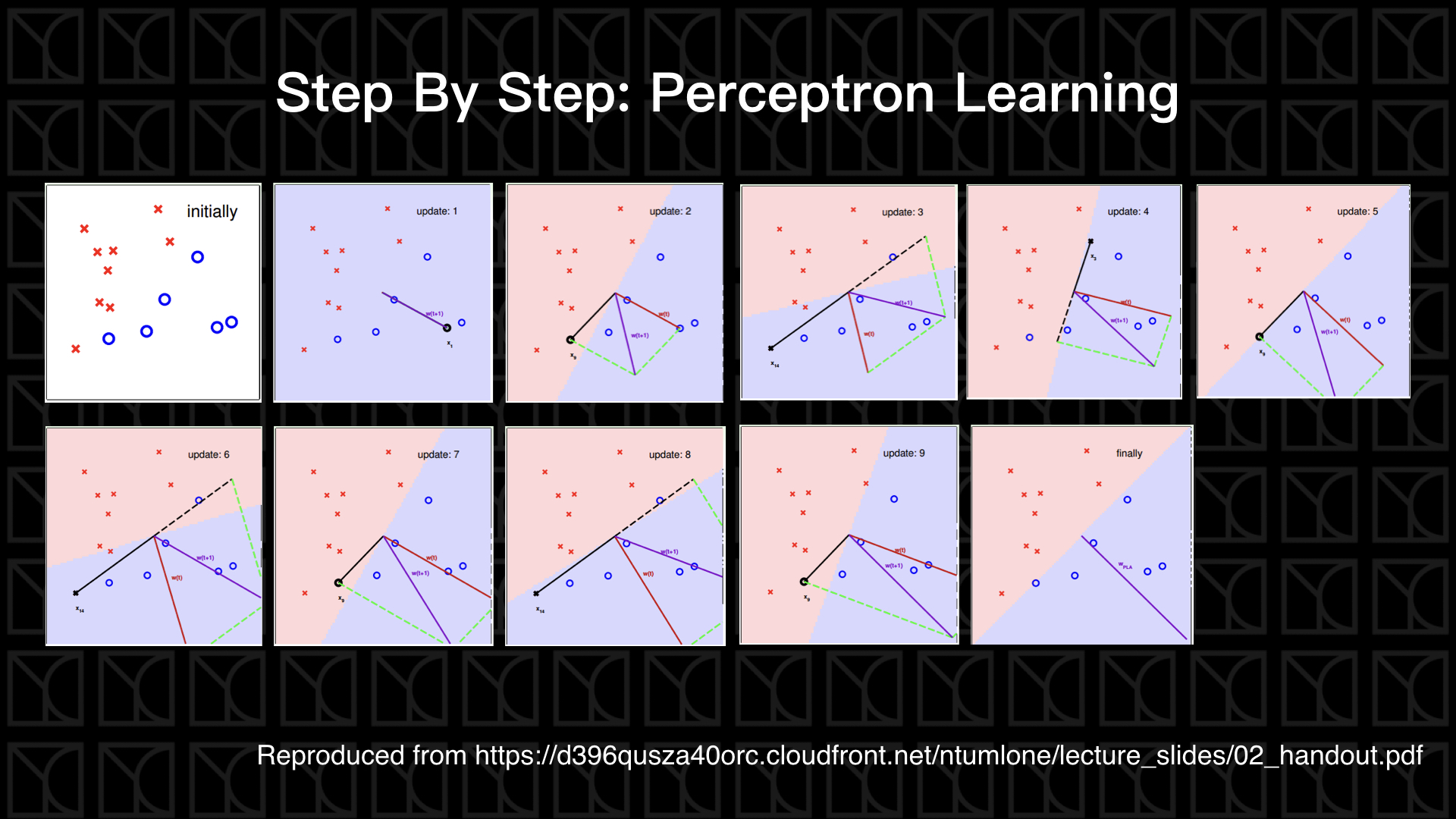
Seeing is believing,上面這張圖帶我們來看PLA如何運作,
- Initially: 在最一開始的時候,我們weight \(W_t\)先設成零向量
- Update 1: PLA更新把零向量的\(W_t\)拉成\(W_{t+1}\)
- Update 2: 上一輪的\(W_{t+1}\)已經是這一輪的\(W_t\),也就是紅色的那個向量,\(W_t\)決定了一條壁壘分明的二元分類邊界,這條線的方程式其實就是 \(w_0+w_1x_1+... = 0\),如果你還記得高中數學的話,這條邊界必然會和\(W_t\)垂直,如圖所示,而\(W_t\)的方向是屬於\(y=+1\)的區域,這一輪剛剛好找到一個圈(\(y=+1\))落在\(y=-1\)的區域,因此我們需要更新weight,做法是把\(W_t\) 和 \(y_n\times X_n\)(=\(X_n\))相加成為新的weight \(W_{t+1}\)
- ...........以此類推
如果資料線性可分的話,PLA在迭代多次後,是可以用一條線完全區分兩種數據。但如果數據不是線性可分,不存在一條線來區分數據,此時最佳解就必須評估整體犯錯有多少,找出犯錯最少的那條直線就是最佳解,但可惜的是PLA方法並不會在迭代中趨向於犯錯最少的那條線,什麼時候該停止迭代是個世紀難解的NP-Hard問題(如果不了解這個名詞,詳見)。
因此要改變一下PLA,這個方法我們稱之為Pocket,當每次得到一組weight的時候,都拿它來評估它對所有Data的區分能力好或壞,而只留下一組最好的放進口袋裡,所以當迭代次數做多了,保留在口袋的這組解就可以看成是最佳解,就這麼簡單。
多元學習
機器學習和人類學習一樣,有各式各樣的學習型態。剛剛的「二元分類問題」就像考「是非題」一樣,答案要嘛是Yes不然就是No,表示為 \(y=\{-1, 1\}\),這就像是機器在小學時代的問題,較為簡單。
現在機器脫離國小來到了國中,考試題目開始出現「選擇題」,這和機器學習中的「多元分類問題」一樣,必須從兩個以上有限的答案中作選擇,表示為 \(y=\{1, 2, ... , k\}\)。
另外機器還可能遇到傷透腦筋的「計算題」,在機器學習裏頭稱為「Regression 問題」,這個時候答案已經放寬到整個實數系了,表示為 \(y∈R\),舉個例子,譬如利用過去天氣的數據去預測明日氣溫,或者利用歷史股價資料預測未來股價,都是Regression的應用。
此時,機器到了大學,開始碰到不那麼容易回答,甚至不存在單一答案的「申論題」,這在ML中像是「Structure Learning 問題」,答案的選擇換成了各種結構,表示為 \(y=\{structures\}\),舉個例子可能比較好理解,例如:自然語言,我們都希望有一天電腦可以理解我們的語言,我們可以不再需要以機器語言來和電腦溝通,而是用人類的語言直接和電腦溝通,聽起來很棒對吧! 這個部分的ML就需要Structure Learning來學習語言的文法結構。
我們教機器學習也有各種不同的教育方法。
有像是填鴨式教育的「Supervised Learning」(監督式學習),直接告訴機器考題和答案,讓機器從中學習,這種情況下每筆資料\(X_n\)對應的\(y_n\)都有明確Label,Data中有明顯的答案。
有像是培養科學家教育方法一樣的「Unsupervised Learning」(非監督式學習),此時每筆資料\(X_n\)對應的\(y_n\)都沒有Label,所以機器要自己歸納整理,然後從中學到規律,通常用於分群問題,對資料做分類找出規律性。
那還有折衷於上述兩種方法的啟發式教育,「Semi-supervised Learning」(半監督式學習),在這個情形下有部分資料\(y_n\)是有Label的,機器可以藉由有Label的正確答案和資料的規律性來做更好的學習,一個有名的例子是Facebook的人臉辨識標記功能,有部分已經被用戶標記的照片,這屬於有Label的\(y_n\),但有更多沒有標記的照片,這些照片也可以幫助ML學習。
那還有像是訓練小狗的方法,當我跟小狗說坐下,如果牠真的坐下了,這個時候我就給牠獎勵,譬如說餵牠好吃的食物,久而久之牠就會學會聽從這個命令,「Reinforcement Learning」(強化式學習)就是不直接表明\(y_n\)的Label,但是機器能在嘗試中得到\(y_n\)結果的好壞,再從這個好壞當作回饋去優化它的學習。
Data給的方法也可以有很多種類。
剛剛舉的ML例子都是屬於「Batch Learning」,也就是一次給你所有的Data。另外一種給Data的方法叫做「Online Learning」,這個情形下Data會一個一個以序列的方式餵給機器,這麼方式下的Model可以隨時更新。最後一種方式是「Active Learning」,機器不僅是被動的接受 Data,而是會根據它自己的需求向使用者索取它想要的Data。
另外,除了有輸出值\(y_n\)有多種種類之外,輸入的變數\(X_n\)的來源也有很多種,我們稱之為Features。
如果具有物理意義的輸入變數,稱之為「Concrete Features」,這些變數建立在人類知識的預先處理。還有輸入變數並不具有物理含意的情形,這稱之為「Abstract Features」。那有些情形下直接採用不加以處理的原始數據,稱為「Raw Features」。
而使用工人智慧由人力從Raw Features中萃取出Concrete Features,這叫做Feature Engineering。相反的,現在很夯的Deep Learning厲害的地方是他可以自行從Data中學習 Features。
總結一下,機器學習有很多種型態,從Data的給予方式可分為Batch Learning、Online Learning和Active Learning。Data的表達形式由輸入變數\(X_n\)和輸出值\(y_n\)所決定,從輸入變數\(X_n\)的來源可分為Concrete Features、Raw Features和Abstract Features,從輸出值\(y_n\)的種類上可以分為二元分類、多元分類、Regression和Structured Learning 問題,從輸出值\(y_n\)的Label給予情況可分為Supervised Learning、Unsupervised Learning、Semi-supervised Learning 和 Reinforcement Learning。
順道一提,這16堂課裡頭主要聚焦在探討Batch Supervised Learning with Concrete Features。
後話
這篇文章帶大家初探了一眼機器學習,介紹了機器學習的架構和種類,以及它的使用時機,還有介紹了整門課非常重要的二元分類問題。但是講這麼多,機器學習真的可能嗎? 那如果可以做到,會需要哪一些要素呢? 這就必須深入理論之中,才能找到答案,在下一篇文章裡,我將介紹這門課的第二個部分:Why Can Machines Learn?