OCR：CRNN+CTC開源加詳細解析

場景文字辨識 OCR (Optical Character Recognition) 應用場景非常多，例如：Evernote提供的名片辨識、諸多銀行內部使用的存摺影像辨識、新型停車場提供的車牌辨識系統、證件識別工具、旅遊業會用到護照識別，不勝枚舉！凡是想要將生活場景中的文字藉由機器去讀取的都是OCR的範疇，它會為企業省下許多人工判讀的人力成本。

在場景文字辨識中相當經典的模型就是 CRNN+CTC，Github 上也有許多相關的 Repo.，但 YC 發現沒有一個將這個模型寫的夠好、夠容易修改的 pytorch 開源程式碼，所以 YC 決定自己幹一個並且將它開源，目前搭配資料集 Synth90k 已經可以在英文辨識上做到 93.9 % 的 Sequence Accuracy，歡迎大家來嘗試使用！

開源：pytorch版本的CRNN+CTC

GitYCC/crnn-pytorch

👆🏼👆🏼👆🏼👆🏼👆🏼

麻煩大家不吝給予星星 ⭐️，並且分享給更多人知道！

網路架構

CRNN+CTC 結構源於論文An End-to-End Trainable Neural Network for Image-based Sequence Recognition and Its Application to Scene Text Recognition (2015), Baoguang Shi et al.，其網路架構其實並不複雜，講白了就是 CNN 的 Backbone 再搭配 Bi-directional RNN，最後對每個時間點作Softmax分類問題，但是在衡量輸出時則是需要綜觀每個時間點的 CTC Loss。

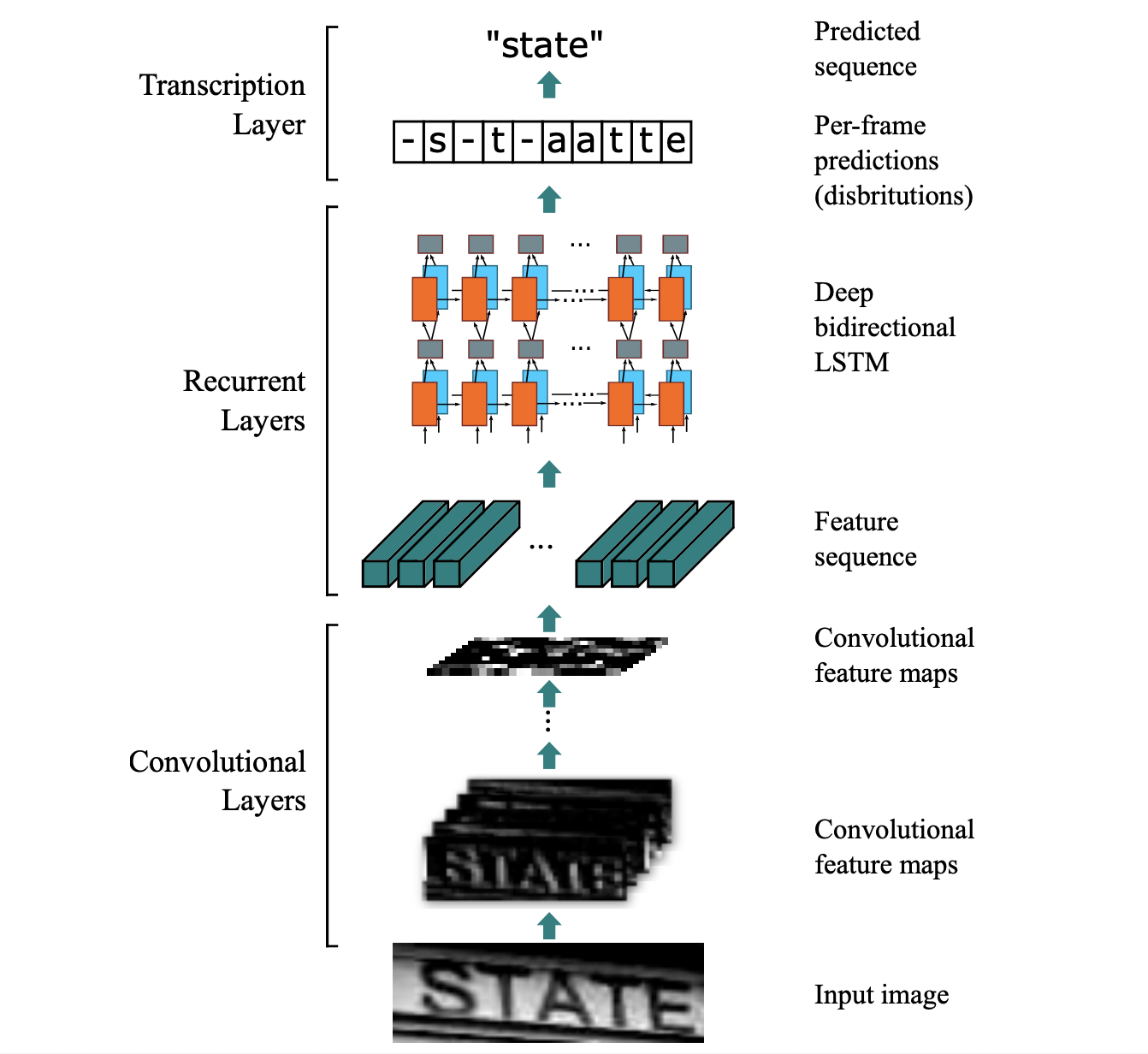
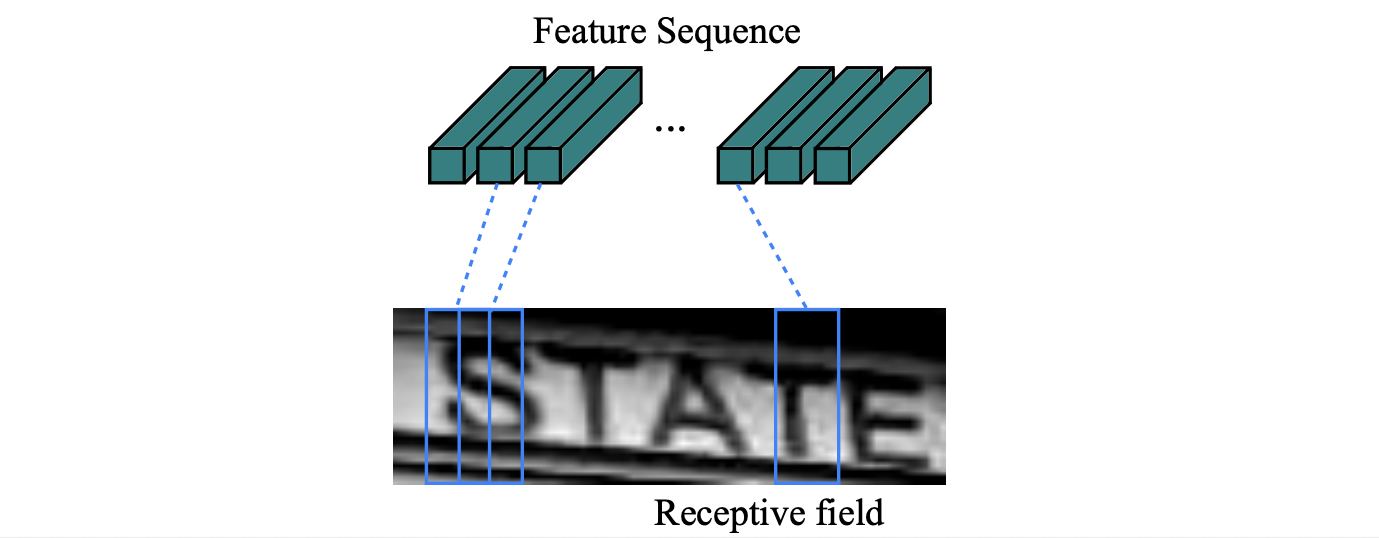
首先，將圖片轉成灰階並且伸縮至高度32，通過多層的Conv2D、MaxPool和BatchNormalization抽取圖片相關的特徵。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

assert img_height % 16 == 0
assert img_width % 4 == 0

channels = [img_channel, 64, 128, 256, 256, 512, 512, 512]
kernel_sizes = [3, 3, 3, 3, 3, 3, 2]
strides = [1, 1, 1, 1, 1, 1, 1]
paddings = [1, 1, 1, 1, 1, 1, 0]

cnn = nn.Sequential()

def conv_relu(i, batch_norm=False):
    # shape of input: (batch, input_channel, height, width)
    input_channel = channels[i]
    output_channel = channels[i+1]

    cnn.add_module(
        f'conv{i}',
        nn.Conv2d(input_channel, output_channel, kernel_sizes[i], strides[i], paddings[i])
    )

    if batch_norm:
        cnn.add_module(f'batchnorm{i}', nn.BatchNorm2d(output_channel))

    relu = nn.LeakyReLU(0.2, inplace=True) if leaky_relu else nn.ReLU(inplace=True)
    cnn.add_module(f'relu{i}', relu)

# size of image: (channel, height, width) = (img_channel, img_height, img_width)
conv_relu(0)
cnn.add_module('pooling0', nn.MaxPool2d(kernel_size=2, stride=2))
# (64, img_height // 2, img_width // 2)

conv_relu(1)
cnn.add_module('pooling1', nn.MaxPool2d(kernel_size=2, stride=2))
# (128, img_height // 4, img_width // 4)

conv_relu(2)
conv_relu(3)
cnn.add_module(
    'pooling2',
    nn.MaxPool2d(kernel_size=(2, 1))
)  # (256, img_height // 8, img_width // 4)

conv_relu(4, batch_norm=True)
conv_relu(5, batch_norm=True)
cnn.add_module(
    'pooling3',
    nn.MaxPool2d(kernel_size=(2, 1))
)  # (512, img_height // 16, img_width // 4)

conv_relu(6)  # (512, img_height // 16 - 1, img_width // 4 - 1)

接下來藉由一個 DenseLayer 去將圖片轉成維度為 map_to_seq_hidden 的序列，這樣就可以接續的使用 RNN 來萃取序列的特徵。

1

self.map_to_seq = nn.Linear(output_channel * output_height, map_to_seq_hidden)

這邊特別注意一下，當你經過 CNN Backbone 之後的維度是：(batch, channel, new_height, new_width) ，但是你希望進RNN前的維度是：(seq_len, batch, map_to_seq_hidden) ，所以需要將 channel, new_height 攤平再過 DenseLayer，如下：

1
2
3

conv = conv.view(batch, channel * height, width)
conv = conv.permute(2, 0, 1)  # (width, batch, feature)
seq = self.map_to_seq(conv)

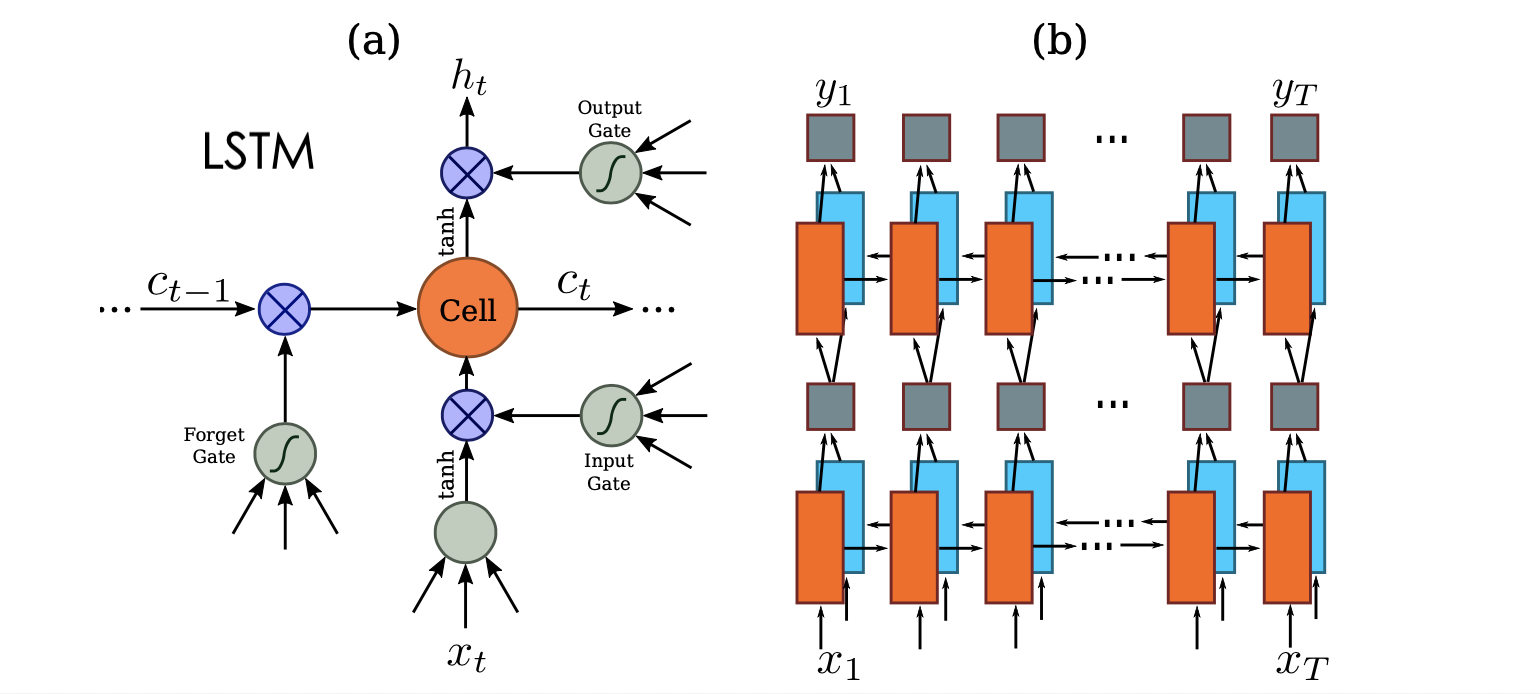
最後再過兩層 Bi-directional LSTM 萃取序列相關的特徵，並且過 DenseLayer 來將維度轉成與分類的數量相同，再過 Softmax 就大功告成！注意：分類的類別是所有要預測的字元再加上 blank ε ，一般我們會讓 blank ε 在Onehot Encoding 時放在 index=0 的位置。

詳細模型架構請詳見：src/model.py

CTC (Connectionist Temporal Classification)

RNNs 與其他傳統方法相比，如：HMMs (Hidden Markov Model) 和 CRFs (Conditional Random Field) 有以下優勢：

• RNNs 無須多餘的先驗假設
• RNNs 提供了相當強大且一般化的機制去描述時間序列

但是 RNNs 只能訓練在已經分配好的序列上，所以當你僅有 Sequence Label 是不夠的，還需要知道這些 Label 要怎麼被分配。舉個例子：如果今天你要辨識的圖片包含 "CAT" 這個詞，你想要使用 RNN 進行辨識，而這個 RNN 長度假設為 7，為了要能訓練 RNN 我們需要給它 Ground True，此時你就需要將 "CAT" 這 3 個字分配到 7 格中，但是這樣的標注是費工的、不切實際的，我們希望可以直接訓練在沒有分配前的 Sequence Label 上。

CTC 設計了一個機制讓我們可以做到這件事：

1. 在原本要預測的字元中多加入了 blank ε
2. 透過映射機制 \(B\) 將 RNN 的輸出轉化成 Sequence Prediction
3. 映射機制 \(B\)：合併相鄰的字元並且除去 blank ε

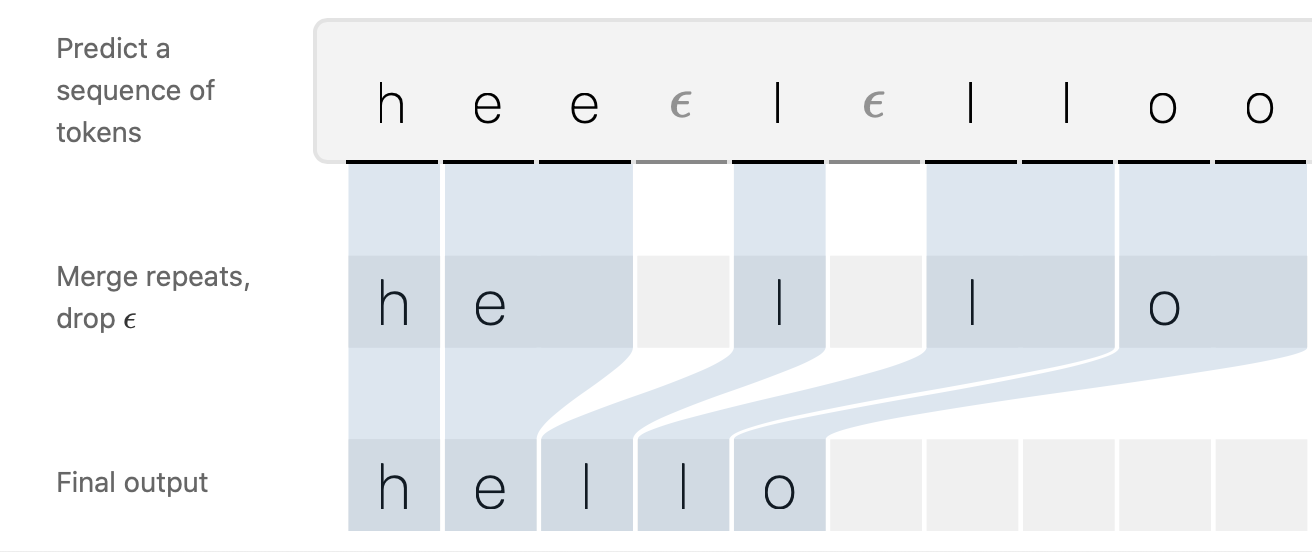
有了這個映射機制 \(B\) 我們就可以不需要事先分配 Sequence Label 也能訓練網路，但是要注意：能映射到一組 Sequence Label 的可能性是有很多組合的，例如："hee-l-lloo" 和 "hheel-lloo" 都會映射到 "hello"，所以要特別去設計它的 Loss 讓其可以考慮各種可能性，這會在下一節中仔細闡述。

CTC Loss: Forward-Backward Algorithm

接下來這一個部分將會是本篇最難理解的部分，而且也最為數學，所以在陷進去數學漩渦之前，我們先來概念性的了解 CTC Loss 究竟是做了什麼。簡言之，我們需要讓 CTC Loss 降低的同時，等同於做到提升產生 Ground True Sequence Label 的機率，而在映射函數 \(B\) 的作用下產生這個 Ground True Sequence Label 會有多種來源組合，這些組合都必須被考慮進去，然後我們有了 CTC Loss 與參數的關係式就可以使用梯度下降進行優化。

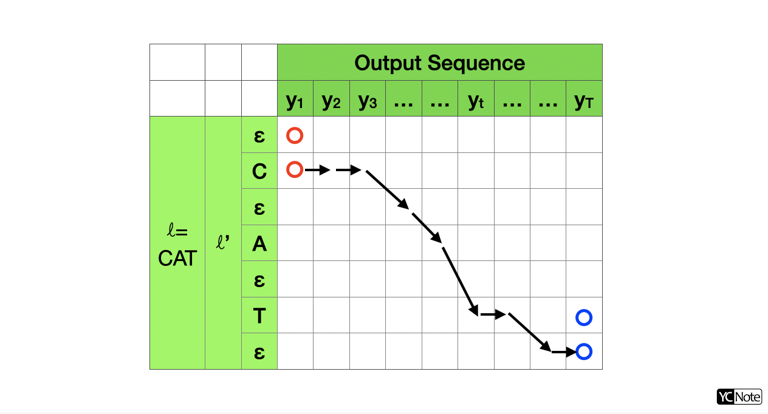
所以我們需要窮舉所有可能的組合才能正確的將產生 Ground True Sequence Label 的機率算出來，我們就來試著羅列。假設我們的 Sequence Label 是 "CAT" ，見圖一，所以我們的 \(\ell\) 為 "CAT"，為了把 blank ε 列入考慮，我們設計了 \(\ell'\)，其長度關係為 \(|\ell'|=2|\ell|+1\) 。參照映射函數的規則，只有圖中兩個紅點是可能的出發點、兩個藍點是可能的結束點，因此我們需要羅列從出發點到結束點可能的路徑 \(\pi\)，這些路徑都可以在經過映射函數 \(B\) 後產生 Sequence Label "CAT" 。

加總所有可能透過 \(B\) 映射至 Ground True Sequence Label \(\ell\) 的條件機率：

其中：

\(y^{t}_{π_t}\) 表示在時間 \(t\) Label 為 \(π_t\) 的機率。

而我們的目標就是想要最大化 \(p(\ell|y)\) ，取 \(ln\) 在加上負號，就會變換成為最小化問題：

只要算其微分，就可以使用梯度下降的方法進行優化：

所以只要解決兩件事：如何計算 \(p(\ell|y)\) 和 \(\frac{\partial p(\ell|y)}{\partial y}\) ，就可以優化參數了！

但是窮舉各種可能路徑有這麼簡單嗎？幸好我們有 Dynamic Programming ，這裡借鏡解 HMM 優化問題會使用的 Forward-Backward Algorithm 來解決這個問題。 Dynamic Programming 是一種遞迴的演算法，只要有初始值和遞迴式就可以一路算下去。運用在這個問題上，我們只需要找到在 \(y_t\) 和 \(y_{t-1}\) 的機率累加遞迴關係，以及 \(y_1\) 時刻的機率分布，就可以一路算到最後一個時刻點 \(T\) 的機率累積。

首先，我們先來定義「Forward Algorithm」的 \(\alpha\) ：

\(\alpha_t(s)\) 表示從可能的起始點累積到 \(t\) 時刻且 Label \(\ell'=s\) 那點的總機率，可以從式子的右式看出，加總所有能將 \(π_{1:t}\) (圖一中的衡欄) 映射到 \(\ell_{1:s}\) (圖一中的縱欄) 的路徑 \(\pi\) ，並且將這路徑 \(\pi\) 上的各點機率相乘 (因為互為獨立事件)。

再參照圖一和【1】式，我們知道 \(p(\ell|y)\) 可以用 \(\alpha_t(s)\) 表示：

右式的兩項代表結束的兩個藍點。

從【5】式我們可以得到 \(t=1\) 的初始值，因為只有兩個紅點是可能的路徑，所以得到：

從【5】式我們也可以得到遞迴式：

連接到 \((t,s)\) 可分為三種路徑情況，如下圖：

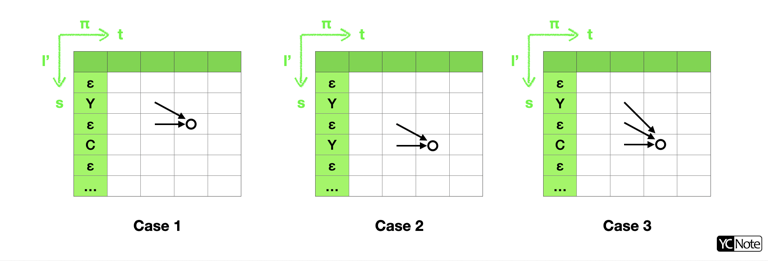
所以我們可以把【8】遞迴式寫得更加清楚：

善用【9】式遞迴式和【7】式初始值，你就可以求得圖一中所有格子的 \(\alpha_t(s)\) 值，再藉由【6】式就可以得到 \(p(\ell|y)\)。

我們順利的解決了【4】式中的 \(p(\ell|y)\)，那接下來只剩下 \(\frac{\partial p(\ell|y)}{\partial y}\)，為了算這一項我們還需要「Backward Algorithm」，「Backward Algorithm」的 \(\beta\) 定義如下：

從【10】式我們可以得到 \(t=T\) 的初始值，因為只有兩個藍點是可能的路徑，所以得到：

從【10】式我們也可以得到遞迴式：

從 \((t,s)\) 連接的情況一樣也可分為三種情況，如下圖：

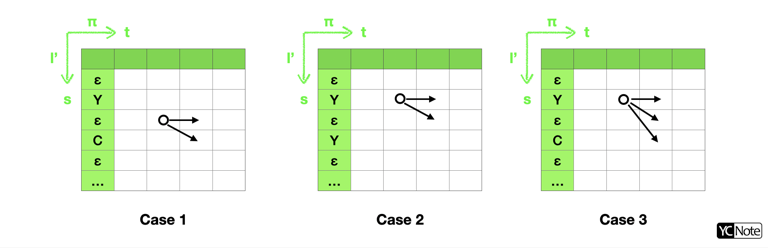
所以我們可以把【12】遞迴式寫得更加清楚：

當我們把 Forward Algorithm 和 Backward Algorithm 合在一起就會得到一個好用的公式，綜【5】和【10】式：

再考慮【2】式

再考慮【1】式

【16】式提供了另外一個求 \(p(\ell|y)\) 的方法，而且這個算法可以在任意時間點 \(t\) 作計算，更棒的是它可以讓我們很方便的求得 \(\frac{\partial p(\ell|y)}{\partial y}\) ：

因為微分的關係，上式加總中與 \(y_k^t\) 無關的項都會化為零，可以進一步改寫：

因此綜【6】和【18】我們就可以解【4】式，然後就可以對網路做反向傳播優化參數了！

Inference of CTC

在 GitYCC/crnn-pytorch 中我有實作了三種 CTC 的 Inference 方法，分別為 greedy_decode、beam_search_decode 和 prefix_beam_decode，精確度依序越來越準確，但是隨著精確度提高所花的 Inference 時間也就越長。

事實上，這三種方式都不是最佳解，真正的最佳解得枚舉出所有可能的 Sequence Label 組合再取最大機率的那一個，它必須要衡量 \((C+1)^T\) 條路徑且每條路徑都需要要做 \(T\) 次的乘法，所以時間複雜度為 \(O(T\times (C+1)^T)\)，這個計算量大到不切實際，假設英文字母 \(C=26\) ，然後 \(T\) 假設為 \(20\)，時間複雜度會達到 \(8.4e\text{+}29\)。

所以接下來我會逐一介紹三種常見的近似方法。

Greedy Decode

這是最 heuristic 的方法，直接找在每個時間點 \(t\) 最大的 \(s\) 當作路徑 \(\pi^*\) 再過映射函數 \(B\)。這個方法雖然簡單，但在大部分情況下會是正確的。在最佳解時我們希望的是在過完映射函數 \(B\) 之後得到最大可能的路徑 \(\ell^*\) ，所以需要考慮所有可能的路徑並將其機率加總才能得到最佳解，但是 Greedy Decode 則是只考慮了最高機率的一條路徑。

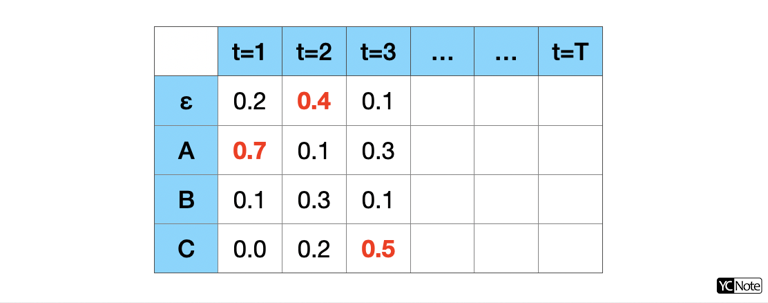
1
2
3
4

def greedy_decode(emission_log_prob, blank=0, **kwargs):
    labels = np.argmax(emission_log_prob, axis=-1)
    labels = _reconstruct(labels, blank=blank)
    return labels

Beam Search Decode

既然只選一條機率最大的路徑不那麼精確，那麼我就選最大的前 \(k\) 條路徑再將其機率相加，這個就是 Beam Search 的近似方法。為了達到這個目的，我們在每一個時間點 \(t\) 都會保留前 \(k\) 條累積相乘機率最大的可能路徑，如下圖所示。

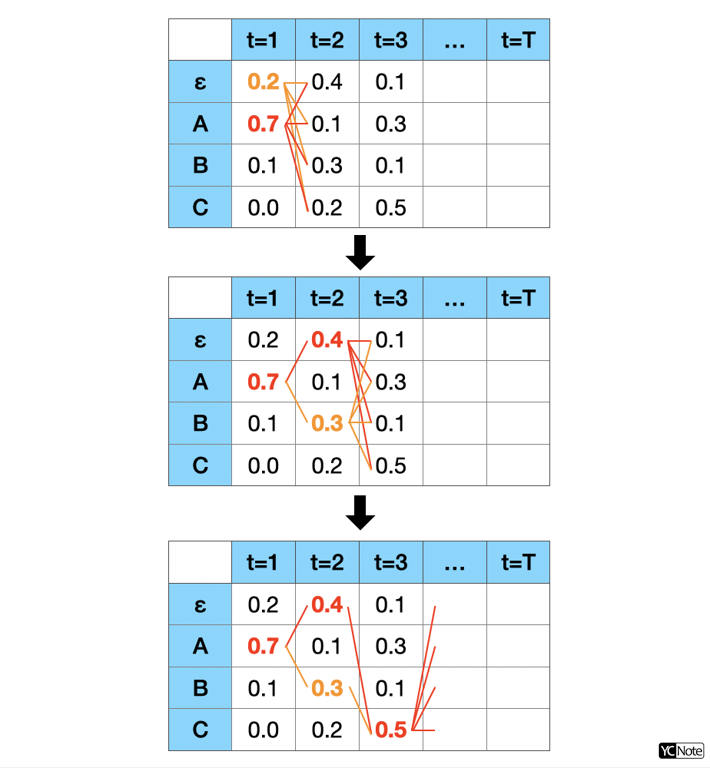
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

def beam_search_decode(emission_log_prob, blank=0, **kwargs):
    beam_size = kwargs['beam_size']
    emission_threshold = kwargs.get('emission_threshold', np.log(DEFAULT_EMISSION_THRESHOLD))

    length, class_count = emission_log_prob.shape

    beams = [([], 0)]  # (prefix, accumulated_log_prob)
    for t in range(length):
        new_beams = []
        for prefix, accumulated_log_prob in beams:
            for c in range(class_count):
                log_prob = emission_log_prob[t, c]
                if log_prob < emission_threshold:
                    continue
                new_prefix = prefix + [c]
                # log(p1 * p2) = log_p1 + log_p2
                new_accu_log_prob = accumulated_log_prob + log_prob
                new_beams.append((new_prefix, new_accu_log_prob))

        # sorted by accumulated_log_prob
        new_beams.sort(key=lambda x: x[1], reverse=True)
        beams = new_beams[:beam_size]

    # sum up beams to produce labels
    total_accu_log_prob = {}
    for prefix, accu_log_prob in beams:
        labels = tuple(_reconstruct(prefix))
        # log(p1 + p2) = logsumexp([log_p1, log_p2])
        total_accu_log_prob[labels] = \
            logsumexp([accu_log_prob, total_accu_log_prob.get(labels, NINF)])

    labels_beams = [(list(labels), accu_log_prob)
                    for labels, accu_log_prob in total_accu_log_prob.items()]
    labels_beams.sort(key=lambda x: x[1], reverse=True)
    labels = labels_beams[0][0]

    return labels

其中用到 logsumexp 的用意是因為我們操作在 Log Probability 上面，雖然機率相乘即是 Log Probability 相加，很方便操作。但是如果碰到需要機率相加時，就需要先取 \(exp\) 還原後再相加再取 \(log\) ，即：\(log(p1 + p2) = logsumexp([log(p1), log(p2)])\)。

Prefix Beam Search Decode

我們可以再進一步讓它更精確一點，剛剛的 Beam Search 是在映射函數 \(B\) 之前找 \(k\) 條路徑，Prefix Beam Search 更進一步拿前 \(k\) 條經過映射函數 \(B\) 後的 Prefix 當作評估的方式 ，如此會更接近我們想要找到映射後的最高機率的 Sequence。

在 Prefix 的世界裡不存在 blank ε，但是 blank ε 卻是會影響 Prefix，例如："A-A" 映射完會是 "AA"，但是 "AA" 映射完則會是 "A" ，所以在 Prefix Beam Search 存在 ProbabilityWithBlank 和 ProbabilityNoBlank 兩種累積機率，這兩種情況分別是結尾有 blank 的累積機率和結尾沒有 blank 的累積機率，特別注意：累積機率代表從開始到目前的總機率。

有了這個概念，我們來看會遇到什麼樣的狀況，並且在每個狀況下我們要怎麼去計算 ProbabilityWithBlank 和 ProbabilityNoBlank ，以下符號 * 代表上一時刻的 prefix，E 代表上一時刻 prefix 的最後一個字元，ε 代表 blank，以下的情況皆是在考慮新字元進來要怎麼去累加 ProbabilityWithBlank 和 ProbabilityNoBlank ：

特別注意，以上初始化是遇到新的字元就假設其後會不帶 blank。

當然每次考慮一個新的時間點，我們都需要去累加可能會產生這個 Prefix 的各種情況，因此在以下的程式碼中，我們的 ProbabilityWithBlank 和 ProbabilityNoBlank 是會迭代累加的。當累積完這個時間點的所有 Prefix 機率後，我們會取前 \(k\) 大機率的 Prefix 留下來繼續往下一個時間點累加，此時要用 ProbabilityWithBlank 和 ProbabilityNoBlank 的合來當作排序的依據。

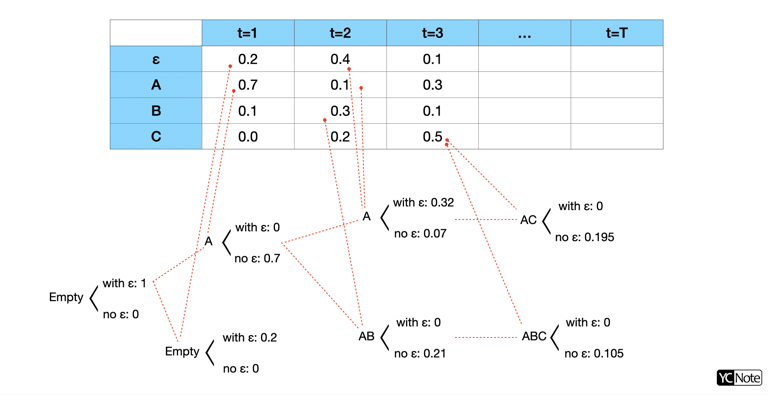
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

def prefix_beam_decode(emission_log_prob, blank=0, **kwargs):
    beam_size = kwargs['beam_size']
    emission_threshold = kwargs.get('emission_threshold', np.log(DEFAULT_EMISSION_THRESHOLD))

    length, class_count = emission_log_prob.shape

    beams = [(tuple(), (0, NINF))]  # (prefix, (blank_log_prob, non_blank_log_prob))
    # initial of beams: (empty_str, (log(1.0), log(0.0)))

    for t in range(length):
        new_beams_dict = defaultdict(lambda: (NINF, NINF))  # log(0.0) = NINF

        for prefix, (lp_b, lp_nb) in beams:
            for c in range(class_count):
                log_prob = emission_log_prob[t, c]
                if log_prob < emission_threshold:
                    continue

                end_t = prefix[-1] if prefix else None

                # if new_prefix == prefix
                new_lp_b, new_lp_nb = new_beams_dict[prefix]

                if c == blank:
                    new_beams_dict[prefix] = (
                        logsumexp([new_lp_b, lp_b + log_prob, lp_nb + log_prob]),
                        new_lp_nb
                    )
                    continue
                if c == end_t:
                    new_beams_dict[prefix] = (
                        new_lp_b,
                        logsumexp([new_lp_nb, lp_nb + log_prob])
                    )

                # if new_prefix == prefix + (c,)
                new_prefix = prefix + (c,)
                new_lp_b, new_lp_nb = new_beams_dict[new_prefix]

                if c != end_t:
                    new_beams_dict[new_prefix] = (
                        new_lp_b,
                        logsumexp([new_lp_nb, lp_b + log_prob, lp_nb + log_prob])
                    )
                else:
                    new_beams_dict[new_prefix] = (
                        new_lp_b,
                        logsumexp([new_lp_nb, lp_b + log_prob])
                    )

        # sorted by log(blank_prob + non_blank_prob)
        beams = sorted(new_beams_dict.items(), key=lambda x: logsumexp(x[1]), reverse=True)
        beams = beams[:beam_size]

    labels = list(beams[0][0])
    return labels

結語

我們在這篇文章當中清楚的了解到 CRNN 的架構，以及 CTC 的架構、訓練的參數優化和其三種 Inference 方法。看完了這些原理，也該動手試玩看看，在 GitYCC/crnn-pytorch 中已經有已經 pretrained 的模型可以使用，不妨跟著以下步驟實際動手玩玩看 OCR 場景辨識吧！

1
2
3
4

git clone https://github.com/GitYCC/crnn-pytorch.git
cd crnn-pytorch/
pip install -r requirements.txt
python src/predict.py demo/*.jpg

Reference

• An End-to-End Trainable Neural Network for Image-based Sequence Recognition and Its Application to Scene Text Recognition (2015), Baoguang Shi et al.
• Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks (2006), Alex Graves et al.
• First-Pass Large Vocabulary Continuous Speech Recognition using Bi-Directional Recurrent DNNs (2014), Awni Y. Hannun et al.
• Sequence Modeling With CTC, Awni Hannun.
• 对《CTC 原理及实现》中的一些算法的解释