生成模型 (Generative Model) 家族
在過去,作為生成模型的 GAN (Generative Adversarial Network) 最廣為人使用,GAN是在2014年由 Goodfellow 所提出來的方法,其結構由兩個網路所組成:生成器網路和鑑別器網路,生成器網路負責生成以假亂真的合成樣本,而鑑別器網路負責仔細區分出真實樣本和合成樣本,經由兩者交替對抗學習,最終我們可以得到一個好的生成器。這個生成器網路通常輸入為一組取樣自高斯分布的亂數,而輸出就是合成樣本。
為何我們需要取樣於一個「分布」?以圖片為例,假設是長32寬32的一張圖片可以由一組長度為32x32x3的向量來表示,這並不意味著一組長度為32x32x3的隨機向量就能產生一張「有意義的」圖片,所以在32x32x3的空間中存在著能產生有意義圖片的不同機率分布,我們只要能把這個機率分布估準了,就可以從這個機率分布抽樣出有意義的圖片,這就是為何生成模型往往需要抽樣至某個分布,可想而知要用簡單的數學式來表示這樣的分布是多們困難的一件事,因此科學家們設計了一個簡單分布—高斯分布,並希望透過若干複雜的轉換(通常使用深度網路)後可以得到這個複雜的分布,通常我們會稱這個高斯分布為Hidden Space,因此「從樣本空間抽樣」等效於「從Hidden Space抽樣再轉換」。
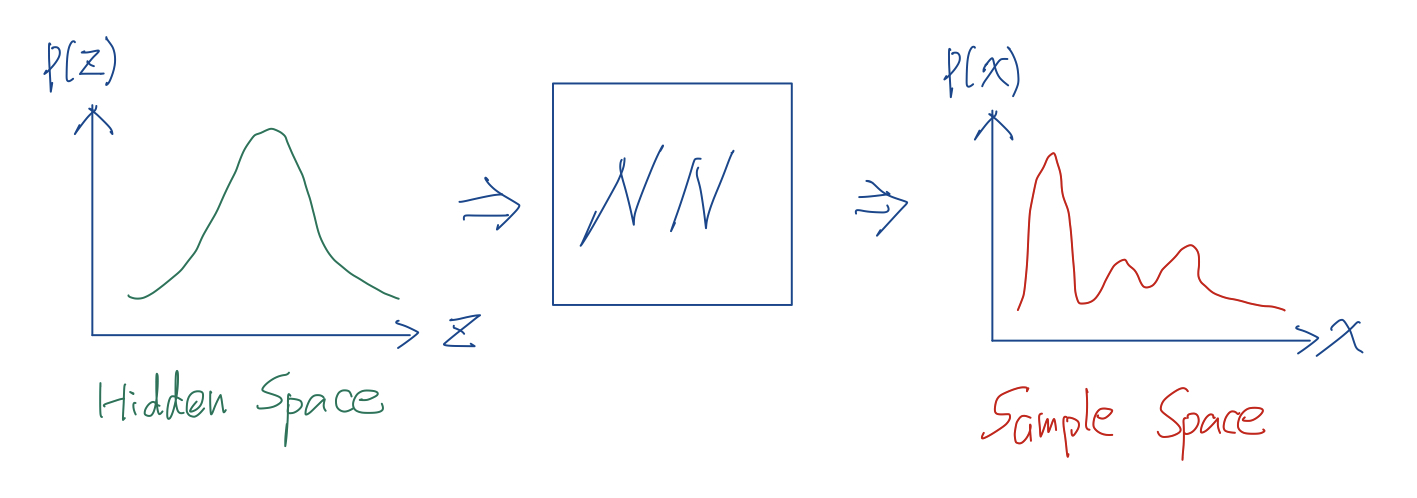
繼GAN以後有一個後起之秀 — Flow-based Generative Model,不同於 GAN 需要一個鑑別器網路來輔助訓練生成器網路,Flow-based Generative Model 透過一個可逆推的網路結構來訓練,這個可逆推網路的兩端就是Hidden Space跟我們想要得到的Sample Space,既然網路是可以逆推的,我們就可以輸入一群真實樣本訓練網路將其分布轉換為高斯分布的Hidden Space,待網路訓練完成我們就可以逆推來作為生成器使用。

近期,生成模型的家族又多了一個新的模型,就是本篇要介紹的擴散模型(Diffusion Model),Diffusion Model 的中心思想是使用若干個微幅轉換來轉換Hidden Space成為Sample Space,如上圖所示, \(\pmb{x}_T\) 代表抽樣自高斯分布Hidden Space的圖片,\(\pmb{x}_0\) 代表抽樣自Sample Space的圖片,從 \(\pmb{x}_0\) 到 \(\pmb{x}_T\) 是模糊化的過程,中間經過若干事先定義好的操作 \(q(\pmb{x}_{t}\mid \pmb{x}_{t-1})\),而生成模型旨於學習模糊化的逆向轉換 \(p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_t)\) ,當我們有了\(p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_t)\) 就可以隨機抽樣自Hidden Space並轉成一張合成的圖片。實際操作上,\(p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_t)\) 是一個神經網路,其輸入為圖片 \(\pmb{x}_t\) 和其所在的step \(t\),其輸出為預測模糊化中被添加的雜訊 \(\pmb{z}_\theta(\pmb{x}_t ,t)\) ,經理論的推導證明:
$$
\pmb{x}_{t-1}=\frac{1}{\sqrt{\bar{\alpha}_t}}(\pmb{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\pmb{z}_\theta(\pmb{x}_t ,t))+\sigma_t\pmb{z}\ \ \text{ ; }\pmb{z}\sim\mathcal{N}(0;\pmb{I})
$$
(詳見【2.22】),因此只要能成功預測隨機數 \(\pmb{z}_\theta(\pmb{x}_t ,t)\) 就可以得到逆推模糊化的反轉換。
閱讀到這裡的你已經把它的概念弄懂八成了,接下來要進入到可怕的數學時間,Are you ready?
從 Variational Inference 到 Evidence Lower Bound (ELBO)
近年來面對極其複雜(e.g. NN)的機率模型,傳統的優化方式變得不可行,如: Expectation-Maximization Algorithm ,所以接下來要跟大家介紹的 Variational Inference (VI) 就變得開始廣為人使用。
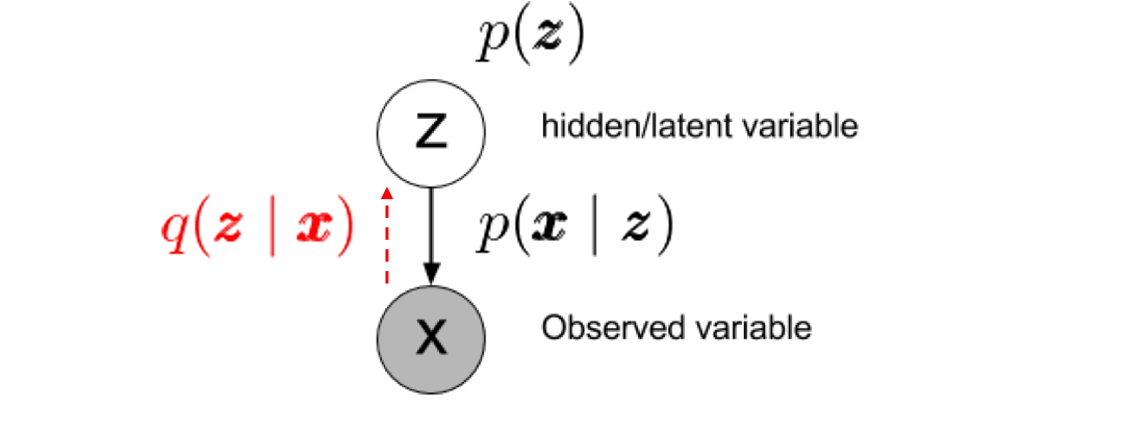
常見的生成模型可以表示成如上圖所示,\(\pmb{x}\) 為生成之樣本,而 \(\pmb{z}\) 座落於 latent space \(Z\) 上的一個點,這個 latent space 可以具有各類可能的分布,為求方便通常會定義為一個 高斯分佈,即 \(p (\pmb{z})\sim\mathcal{N}(\pmb{z}:\pmb{0};\pmb{I})\) 。假設 \(p (\pmb{x}\mid \pmb{z})\) (給定\(\pmb{z}\) 之後求 \(\pmb{x}\) 的分布) 是已知的,則聯合機率為
$$
p (\pmb{x},\pmb{z})=p (\pmb{x}\mid \pmb{z})p (\pmb{z}) \ \ 【1.1】
$$
也可推得
$$
p(\pmb{z}\mid \pmb{x})=\frac{p (\pmb{x},\pmb{z})}{p (\pmb{x})} \ \ 【1.2】
$$
【1.2】是無法輕易求得的,這是雞生蛋蛋生雞的問題,分母的 \(p(\pmb{x})\) 不正是我們想要學習的目標,所以在缺乏這一項的情況下求取 \(p(\pmb{z}\mid \pmb{x})\) 是做不到的。
Variational Inference 的技巧就是引入 \(q(\pmb{z}\mid \pmb{x})\) 來近似 \(p(\pmb{z}\mid \pmb{x})\),這麼做可以得到一個較易計算的 Evidence Lower Bound (ELBO)。接下來我們來推導一下,由於我們希望 \(q(\pmb{z}\mid \pmb{x})\) 和 \(p(\pmb{z}\mid \pmb{x})\)分布盡可能的靠近,所以需要最小化他們之間的 KL Divergence:
$$
min\ D_{KL}[q(\pmb{z}\mid \pmb{x})\mid\mid p(\pmb{z}\mid \pmb{x})] \ \ 【1.3】
$$
其中:
$$
D_{KL}[q(\pmb{z}\mid \pmb{x})\mid\mid p(\pmb{z}\mid \pmb{x})]\\
= \int q(\pmb{z}\mid \pmb{x})\ log\ \frac{q(\pmb{z}\mid \pmb{x})}{p(\pmb{z}\mid \pmb{x})}d\pmb{z}\\
= \int q(\pmb{z}\mid \pmb{x})\ log\ \frac{p(\pmb{x})q(\pmb{z}\mid \pmb{x})}{p(\pmb{x},\pmb{z})}d\pmb{z}\ \ \ \text{;因為 }p(\pmb{x},\pmb{z})=p (\pmb{z}\mid \pmb{x})p(\pmb{x})\\
=log\ p(\pmb{x})-\int q(\pmb{z}\mid \pmb{x})\ log\ \frac{p(\pmb{x},\pmb{z})}{q(\pmb{z}\mid \pmb{x})}d\pmb{z}
$$
其中:
$$
ELBO_{\pmb{x},\pmb{z}}=\int q (\pmb{z}\mid \pmb{x})\ log\ \frac{p(\pmb{x},\pmb{z})}{q(\pmb{z}\mid \pmb{x})}d\pmb{z} \ \ 【1.4】
$$
這一項被稱為 Evidence Lower Bound (ELBO),因為 \(p(\pmb{x})\) 是樣本空間機率,應該是一個上帝決定好的定值,所以如果想要讓 \(q(\pmb{z}\mid \pmb{x})\) 和 \(p(\pmb{z}\mid \pmb{x})\)分布盡可能的靠近,就需要最大化ELBO。而這項是可以計算的,將其寫成抽樣估計的形式:
$$
ELBO_{\pmb{x},\pmb{z}}=E_{q (\pmb{z}\mid \pmb{x})}[log\ \frac{p(\pmb{x}\mid\pmb{z})p(\pmb{z})}{q(\pmb{z}\mid \pmb{x})}]\ \ 【1.5】
$$
上式中的 \(p(\pmb{z})\) 是定義好的分布,通常為高斯分布,\(p(\pmb{x}\mid\pmb{z})\) 和 \(q(\pmb{z}\mid \pmb{x})\) 也是兩個已知的函式,所以【1.5】是可求得的。
回過頭來看Diffusion Model,每一個 Step 中模糊化 \(q(\pmb{x}_{t}\mid \pmb{x}_{t-1})\) 與逆模糊化 \(p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_t)\) 應該存在ELBO的限制,在待會的推倒中我們會看到這一點。
擴散模型的Loss Function
接著我們來完整推導Diffusion Model 吧!每一次的模糊化我們可以定義為
$$
q(\pmb{x}_t\mid\pmb{x}_{t-1})=\mathcal{N}(\pmb{x}_t:\sqrt{1-\beta_t}\pmb{x}_{t-1};\beta_t\pmb{I}) \ \ 【2.1】
$$
其中 \(\beta\)是介於0到1之間,這項可以是學來的,也可以是事前定義的定值,在 DDPM 論文中,\(\beta\) 是一個定好的值。而經過 \(T\) 次(事先定義)的模糊化後,我們希望最終的 \(\pmb{x}_T\) 可以接近高斯分布,即:
$$
\pmb{x}_T\sim\mathcal{N}(\pmb{x}_T:0;\pmb{I}) \ \ 【2.2】
$$
這個過程我們稱之為正向擴散過程(forward diffusion process)。而逆模糊化我們定義成:
$$
p_\theta (\pmb{x}_{t-1}\mid\pmb{x}_{t})\sim\mathcal{N}(\pmb{x}_{t-1}:\pmb{\mu}_\theta (\pmb{x}_t ,t);\pmb{\Sigma}_\theta (\pmb{x}_t ,t)) \ \ 【2.3】
$$
其中 \(p_\theta (\pmb{x}_{t-1}\mid\pmb{x}_{t})\) 用來近似 \(q(\pmb{x}_{t-1}\mid\pmb{x}_{t})\),\(\pmb{\mu}_\theta\) 和 \(\pmb{\Sigma}_\theta\) 代表模型 \(\theta\) 預測的平均值和標準差。
然而模糊化 \(q(\pmb{x}_{t}\mid \pmb{x}_{t-1})\) 與逆模糊化 \(p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_t)\) 應該存在ELBO的限制,從 【1.4】出發:
$$
ELBO_{\pmb{x}_{0:T}}=\int q (\pmb{x}_{1:T}\mid \pmb{x}_0)\ log\ \frac{p_{\theta}(\pmb{x}_{0:T})}{q (\pmb{x}_{1:T}\mid \pmb{x}_0)}d\pmb{x}_{1:T}\\
=-\int q (\pmb{x}_{1:T}\mid \pmb{x}_0)\ [log\frac{q (\pmb{x}_{T}\mid \pmb{x}_{0})}{p_{\theta}(\pmb{x}_{T})}+\sum_{t=2}^{T}log\frac{q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})}{p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_{t})}-log\ p_\theta(\pmb{x}_{0}\mid \pmb{x}_{1})]d\pmb{x}_{1:T}\\
=-\{D_{KL}[q (\pmb{x}_{T}\mid \pmb{x}_{0})\mid\mid p_{\theta}(\pmb{x}_{T})]+\sum_{t=2}^{T}D_{KL}[q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})\mid\mid p_{\theta}(\pmb{x}_{t-1}\mid\pmb{x}_{t})]-log\ p_\theta(\pmb{x}_{0}\mid \pmb{x}_{1})\} \ \ 【2.4】
$$
其中:
$$
log\ \frac{p_{\theta}(\pmb{x}_{0:T})}{q (\pmb{x}_{1:T}\mid \pmb{x}_0)}\\
=-log\ \frac{q (\pmb{x}_{1:T}\mid \pmb{x}_0)}{p_{\theta}(\pmb{x}_{0:T})}\\
=-log\ \frac{\prod_{t=1}^{T} q (\pmb{x}_{t}\mid \pmb{x}_{t-1})}{p_{\theta}(\pmb{x}_{T})\prod_{t=1}^{T}p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_{t})}\\
=-[-log\ p_{\theta}(\pmb{x}_{T})+\sum_{t=1}^{T}log\frac{q (\pmb{x}_{t}\mid \pmb{x}_{t-1})}{p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_{t})}]\\
=-[-log\ p_{\theta}(\pmb{x}_{T})+\sum_{t=2}^{T}log\frac{q (\pmb{x}_{t}\mid \pmb{x}_{t-1})}{p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_{t})}+log\frac{q (\pmb{x}_{1}\mid \pmb{x}_{0})}{p_\theta(\pmb{x}_{0}\mid \pmb{x}_{1})}] \\
=-[-log\ p_{\theta}(\pmb{x}_{T})+\sum_{t=2}^{T}log\frac{q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})}{p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_{t})}\frac{q (\pmb{x}_{t}\mid \pmb{x}_{0})}{q(\pmb{x}_{t-1}\mid \pmb{x}_{0})}+log\frac{q (\pmb{x}_{1}\mid \pmb{x}_{0})}{p_\theta(\pmb{x}_{0}\mid \pmb{x}_{1})}]\\
\text{;因為 }q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})=\frac{q (\pmb{x}_{t-1}, \pmb{x}_{t},\pmb{x}_{0})}{q (\pmb{x}_{t},\pmb{x}_{0})}=\frac{q (\pmb{x}_{t}\mid\pmb{x}_{t-1})q (\pmb{x}_{t-1}\mid\pmb{x}_{0})q (\pmb{x}_{0})}{q (\pmb{x}_{t}\mid\pmb{x}_{0})q (\pmb{x}_{0})}\\
=-[-log\ p_{\theta}(\pmb{x}_{T})+\sum_{t=2}^{T}log\frac{q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})}{p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_{t})}+\sum_{t=2}^{T}log\frac{q (\pmb{x}_{t}\mid \pmb{x}_{0})}{q(\pmb{x}_{t-1}\mid \pmb{x}_{0})}+log\frac{q (\pmb{x}_{1}\mid \pmb{x}_{0})}{p_\theta(\pmb{x}_{0}\mid \pmb{x}_{1})}]\\
=-[-log\ p_{\theta}(\pmb{x}_{T})+\sum_{t=2}^{T}log\frac{q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})}{p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_{t})}+log\frac{q (\pmb{x}_{T}\mid \pmb{x}_{0})}{q(\pmb{x}_{1}\mid \pmb{x}_{0})}+log\frac{q (\pmb{x}_{1}\mid \pmb{x}_{0})}{p_\theta(\pmb{x}_{0}\mid \pmb{x}_{1})}]\\
=-[log\frac{q (\pmb{x}_{T}\mid \pmb{x}_{0})}{p_{\theta}(\pmb{x}_{T})}+\sum_{t=2}^{T}log\frac{q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})}{p_\theta(\pmb{x}_{t-1}\mid \pmb{x}_{t})}-log\ p_\theta(\pmb{x}_{0}\mid \pmb{x}_{1})]
$$
我們需要最大化ELBO,從【2.4】可得優化任務為:
$$
\theta^*=\text{argmin}_{\theta}\ -ELBO_{\pmb{x},\pmb{z}}=\text{argmin}_{\theta}\{L_T+L_{T-1}+...+L_{1}+L_0\} \ \ 【2.5】
$$
其中:
$$
L_T=D_{KL}[q (\pmb{x}_{T}\mid \pmb{x}_{0})\mid\mid p_{\theta}(\pmb{x}_{T})] \ \ 【2.6】
$$
$$
L_{1\leq t\leq T-1}=D_{KL}[q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})\mid\mid p_{\theta}(\pmb{x}_{t-1}\mid\pmb{x}_{t})] \ \ 【2.7】
$$
$$
L_0=-log\ p_\theta(\pmb{x}_{0}\mid \pmb{x}_{1}) \ \ 【2.8】
$$
計算\(L_T\)
\(L_T\) 與 \(\theta\) 無關,不需要優化,可以忽略。
計算\(L_0\)
因為【2.3】,所以 \(p_\theta(\pmb{x}_0\mid\pmb{x}_1)\) 是可以由模型預測而得的。
計算\(L_{1\leq t\leq T-1}\)
\(L_t\) 這一項先從 \(q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})\) 開始做起,先給公式後面再補上證明:
$$
q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})=\mathcal{N}(\pmb{x}_{t-1}:\tilde{\pmb{\mu}}_t (\pmb{x}_t ,\pmb{x}_0);\tilde{\beta}_t\pmb{I}) \ \ 【2.9】
$$
其中:
$$
\tilde{\pmb{\mu}}_t (\pmb{x}_t ,\pmb{x}_0)=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_{t}}\pmb{x}_0+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{(1-\bar{\alpha}_{t})}\pmb{x}_t \ \ 【2.10】
$$
$$
\tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_t \ \ 【2.11】
$$
$$
\alpha_t=1-\beta_t \ \ 【2.12】
$$
$$
\bar{\alpha}_t=\prod_{s=1}^t\alpha_s \ \ 【2.13】
$$
接下來回過頭來,我們要來證明【2.9】,在那之前我們要來證明一個好用的式子,由【2.1】搭配【2.12】、【2.13】置換變數可得
$$
\pmb{x}_t=\sqrt{\alpha_t}\pmb{x}_{t-1}+\sqrt{1-\alpha_t}\pmb{\epsilon}_{t-1}\\
=\sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}\pmb{x}_{t-2}+\sqrt{1-\alpha_{t-1}}\pmb{\epsilon}_{t-2})+\sqrt{1-\alpha_t}\pmb{\epsilon}_{t-1} \\
=\sqrt{\alpha_t\alpha_{t-1}}\pmb{x}_{t-2}+[\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}\pmb{\epsilon}_{t-2}+\sqrt{1-\alpha_t}\pmb{\epsilon}_{t-1}]\\
=\sqrt{\alpha_t\alpha_{t-1}}\pmb{x}_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}\bar{\pmb{\epsilon}}_{t-2}\\
...\\
=\sqrt{\bar{\alpha}_t}\pmb{x}_{0}+\sqrt{1-\bar{\alpha}_t}\pmb{\epsilon}\text{ ; }\pmb{\epsilon}\sim\mathcal{N}(0;\pmb{I}) \ \ 【2.14】\\
\Rightarrow q (\pmb{x}_{t}\mid \pmb{x}_{0})=\mathcal{N}(\sqrt{\bar{\alpha}_t}\pmb{x}_{0};(1-\bar{\alpha}_t)\pmb{I}) \ \ 【2.15】
$$
上式中 \(\bar{\epsilon}\) 代表兩個 Guaissan 的相加,其分布遵循 \(\sum_{i=1}^{n}a_i\cdot \mathcal{N}(z:\mu_i;\sigma^2_i)=\mathcal{N}(z:\sum_{i=1}^{n}a_i\mu_i;\sum_{i=1}^{n}a_i^2\sigma_i^2)\)。
如此一來就可以來計算目標了,引入【2.1】、【2.15】可得
$$
q (\pmb{x}_{t-1}\mid \pmb{x}_{t},\pmb{x}_{0})=q (\pmb{x}_{t}\mid \pmb{x}_{t-1},\pmb{x}_{0})\frac{q (\pmb{x}_{t-1}\mid \pmb{x}_{0})}{q (\pmb{x}_{t}\mid \pmb{x}_{0})}\\
\propto exp\{-\frac{1}{2}[\frac{(\pmb{x}_{t}-\sqrt{\alpha_t}\pmb{x}_{t-1})^2}{\beta_t}+\frac{(\pmb{x}_{t-1}-\sqrt{\bar{\alpha}_{t-1}}\pmb{x}_{0})^2}{1-\bar{\alpha}_{t-1}}-\frac{(\pmb{x}_{t}-\sqrt{\bar{\alpha}_{t}}\pmb{x}_{0})^2}{1-\bar{\alpha}_{t}}]\}\\
=exp\{-\frac{1}{2}[(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}})\pmb{x}_{t-1}^2-(\frac{2\sqrt{\alpha_t}}{\beta_t}\pmb{x}_{t}+\frac{2\sqrt{\bar{\alpha}_t}}{1-\bar{\alpha}_t}\pmb{x}_{0})\pmb{x}_{t-1}+C(\pmb{x}_{t},\pmb{x}_{0})]\}
$$
整理可得平均值和方差為【2.10】和【2.11】。
接下來為求方便計算,我們假設 \(\pmb{\Sigma}_{\theta}\) 為:
$$
\pmb{\Sigma}_\theta (\pmb{x}_t ,t)=\sigma_{t,\theta} \pmb{I} \ \ 【2.16】
$$
【2.16】、【2.9】、【2.3】和【A.1】代入【2.7】可得
$$
L_{1\leq t\leq T-1}=D_{KL}[\mathcal{N}(\pmb{x}_{t-1}:\tilde{\pmb{\mu}}_t (\pmb{x}_t ,\pmb{x}_0);\tilde{\beta}_t\pmb{I})\mid\mid \mathcal{N}(\pmb{x}_{t-1}:\pmb{\mu}_\theta (\pmb{x}_t ,t);\pmb{\Sigma}_\theta (\pmb{x}_t ,t))] \\
=\sum_{j=1}^{J} D_{KL}[\mathcal{N}(x_{t-1,j}:\tilde{\mu}_{t,j} (\pmb{x}_t ,\pmb{x}_0);\tilde{\beta}_{t,j})\mid\mid \mathcal{N}(x_{t-1,j}:\mu_{\theta,j} (\pmb{x}_t ,t);\sigma_{t,\theta} (\pmb{x}_t ,t)\pmb{I})]\\
=\sum_{j=1}^{J} log\frac{\sigma_{t,\theta}}{\tilde{\beta}_{t,j}}+\frac{\tilde{\beta}_{t,j}^2+[\tilde{\mu}_{t,j} (\pmb{x}_t ,\pmb{x}_0)-\mu_{\theta,j} (\pmb{x}_t ,t)]^2}{2\sigma_{t,\theta}^2}-\frac{1}{2} \ \ 【2.17】
$$
其中:\(\sigma_{t,\theta}\) 這一項在DDPM當中設為定值,作者實驗了兩種假設 \(\sigma_{t,\theta}=\beta_t\) 和 \(\sigma_{t,\theta}=\tilde{\beta}_t\) 發現對成效來說沒太大的差別。而Improved DDPM這一項則是用學的,作者假設 \(\sigma_{t,\theta}=exp(v\ log\beta_t+(1-v)\ log\tilde{\beta}_t)\)。
觀察【2.17】可發現平均值的優化:
$$
L_{t,mean}=\frac{1}{2\sigma_{t,\theta}^2}[\tilde{\pmb{\mu}}_{t} (\pmb{x}_t ,\pmb{x}_0)-\pmb{\mu}_{\theta} (\pmb{x}_t ,t)]^2\ \ 【2.18】
$$
其中:
$$
\tilde{\pmb{\mu}}_{t} (\pmb{x}_t ,\pmb{x}_0) =\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_{t}}\pmb{x}_0+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{(1-\bar{\alpha}_{t})}\pmb{x}_t
$$
我們可以藉由變換上式來得到優化目標,我們可以優化還原狀況(也就是原圖 \(\pmb{x}_0\)),也可以預測添加的雜訊,而 DDPM作者實驗發現預測添加的雜訊得到的效果比較好,因此我們使用【2.14】替換掉 \(\pmb{x}_0\):
$$
=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_{t}}\times\frac{1}{\sqrt{\bar{\alpha}_t}}[\pmb{x}_t-\sqrt{1-\bar{\alpha}_t}\pmb{\epsilon}]+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{(1-\bar{\alpha}_{t})}\pmb{x}_t\\
=\frac{1}{\sqrt{\bar{\alpha}_t}}(\pmb{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\pmb{\epsilon})\ \ 【2.19】
$$
【2.18】式中 \(\pmb{\mu}_{\theta} (\pmb{x}_t ,t)\) 是我們可以假設的,假設我讓它預測添加的雜訊,我們可以假設為
$$
\pmb{\mu}_{\theta} (\pmb{x}_t ,t)=\frac{1}{\sqrt{\bar{\alpha}_t}}(\pmb{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\pmb{z}_\theta(\pmb{x}_t ,t)) \ \ 【2.20】
$$
因此,我們可以推得逆模糊的關鍵公式,【2.20】代入【2.3】得:
$$
p_\theta (\pmb{x}_{t-1}\mid\pmb{x}_{t})\sim\mathcal{N}(\pmb{x}_{t-1}:\frac{1}{\sqrt{\bar{\alpha}_t}}(\pmb{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\pmb{z}_\theta(\pmb{x}_t ,t));\pmb{\Sigma}_\theta (\pmb{x}_t ,t)) \ \ 【2.21】
$$
上式也可以寫作:
$$
\pmb{x}_{t-1}=\frac{1}{\sqrt{\bar{\alpha}_t}}(\pmb{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\pmb{z}_\theta(\pmb{x}_t ,t))+\sigma_t\pmb{z}\ \ \text{ ; }\pmb{z}\sim\mathcal{N}(0;\pmb{I}) \ \ 【5.22】
$$
【2.19】和【2.20】代入【2.18】得
$$
L_{t,mean}=\frac{\beta^2_t}{2\bar{\alpha}_t(1-\bar{\alpha}_t)\sigma_{t,\theta}^2}\mid\mid\pmb{\epsilon}-\pmb{z}_\theta(\sqrt{\bar{\alpha}_t}\pmb{x}_{0}+\sqrt{1-\bar{\alpha}_t}\pmb{\epsilon},t)\mid\mid^2\ \ 【2.23】
$$
在DDPM中,作者發現使用去除上式Weighting的優化式效果更好,寫作:
$$
L_{t,mean,simple}=\mid\mid\pmb{\epsilon}-\pmb{z}_\theta(\sqrt{\bar{\alpha}_t}\pmb{x}_{0}+\sqrt{1-\bar{\alpha}_t}\pmb{\epsilon},t)\mid\mid^2\ \ 【2.24】
$$
因此DDPM的訓練和取樣示例代碼如下:

其中應用到【2.24】和【2.22】。
Appendix A: KL Divergence between two Gaussians
$$
D_{KL}[\mathcal{N}(z:\mu_1;\sigma^2_1)\mid\mid\mathcal{N}(z:\mu_2;\sigma^2_2)]\\
=\int \mathcal{N}(z:\mu_1;\sigma^2_1)[log\ \mathcal{N}(z:\mu_1;\sigma^2_1)-log\ \mathcal{N}(z:\mu_2;\sigma^2_2)]dz\\
=\int \mathcal{N}(z:\mu_1;\sigma^2_1)\{-\frac{1}{2}[log\ 2\pi\cdot \sigma^2_1+\frac{(z-\mu_1)^2}{\sigma_1^2}]+\frac{1}{2}[log\ 2\pi\cdot \sigma^2_2+\frac{(z-\mu_2)^2}{\sigma_2^2}]\}dz \\
\text{;因為 }\mathcal{N}(\mu;\sigma^2)=\frac{1}{\sqrt{2\pi\cdot \sigma^2}}exp(-\frac{(z-\mu)^2}{2\sigma^2})\\
=-\frac{1}{2}[log\ 2\pi\cdot \sigma^2_1+\frac{(\sigma_1^2+\mu_1^2)-2\mu_1\mu_1+\mu_1^2}{\sigma_1^2}]+\frac{1}{2}[log\ 2\pi\cdot \sigma^2_2+\frac{(\sigma_1^2+\mu_1^2)-2\mu_2\mu_1+\mu_2^2}{\sigma_2^2}] \\
\text{;因為 }\int z\cdot\mathcal{N}(\mu;\sigma^2)dz=\mu\text{ 且 }\int z^2\cdot\mathcal{N}(\mu;\sigma^2)dz=\sigma^2+\mu^2\\
=log\frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2} \ \ 【A.1】
$$
Reference
- Auto-Encoding Variational Bayes: https://arxiv.org/pdf/1312.6114.pdf
- An Introduction to Variational Inference: https://arxiv.org/pdf/2108.13083.pdf
- From Autoencoder to Beta-VAE: https://lilianweng.github.io/posts/2018-08-12-vae/
- Denoising Diffusion Probabilistic Models: https://arxiv.org/pdf/2006.11239.pdf
- What are Diffusion Models: https://lilianweng.github.io/posts/2021-07-11-diffusion-models/



