剖析深度學習 (1)：為什麼Normal Distribution這麼好用？

Posted on February 18, 2020 in AI.ML. View: 13,009

深度學習發展至今已經有相當多好用的套件，使得進入的門檻大大的降低，因此如果想要快速的實作一些深度學習或機器學習，通常是幾行程式碼可以解決的事。但是，如果想要將深度學習或機器學習當作一份工作，深入了解它背後的原理和數學是必要的，才有可能因地制宜的靈活運用，YC準備在這一系列當中帶大家深入剖析深度學習。

首先第一講，我們來聊一個最常見的分布—正態分布（Normal Distribution），也稱為高斯分布（Gaussian Distribution）。

如果你已經學了好一陣子的機器學習或深度學習，應該對於Normal Distribution不陌生，但是你真的懂Normal Distribution嗎？

為什麼Normal Distribution通常作為雜訊的分布？
為何在DL（deep learning），參數的初始化要用Normal Distribution？
為何在Bayesian公式裡常常會使用Normal Distribution當作Prior Probability？
在使用GAN（generative adversarial network）時，為什麼給予的輸入要假設Normal Distribution？

如果你不知道為什麼使用Normal Distribution，你用起來不會怕嗎？這一講我想要回答的是：為什麼Normal Distribution這麼好用？甚至已經到了無腦用的程度，我會從統計學和資訊理論來回答這個問題。

Courtesy Nas Mouti

認識Normal Distribution

首先來看看Normal Distribution的數學表示式

$$ p_{normal}(x)=\frac{1}{\sqrt{2\pi}\sigma}exp\{{-\frac{1}{2\sigma^2}(x-\mu)^2}\} \ \ ↪︎【1】 $$

其中：$\mu$ 剛好是Normal Distribution的 Mean（平均值），$\sigma^2$ 剛好是Normal Distribution的 Variance（方差），來證明一下吧！

證明之前，先來了解什麼是「期望值」，期望值指的是在相同場景下隨機試驗多次，所有那些可能狀態的平均結果。期望值 $E[g(x)]$ 跟兩件事有關：試驗的物理量 $g(x)$ 和試驗的出現機率 $p(x)$ 。

連續形式寫成：

$$ E[g(x)]\equiv\int^{\infty}_{-\infty}g(x)\cdot p(x)dx \ \ ↪︎【2】 $$

另外期望值也有離散的形式：

$$ E[g]\equiv \sum_{i}g_i\cdot p_i \ \ ↪︎【3】 $$

上面兩個式子有個前提是已知機率分布 $p(x)$ 或 $p_i$ 的情況下才能使用，如果今天我們不知道機率分布，只能使用實驗的方法求近似的期望值，此時$p_i$可以用採樣來取代，則變換式【3】為以下公式：

$$ E[g]= \frac{1}{N}\sum_{i=1}^{N}g_i \ \ ↪︎【4】 $$

請大家牢記上面三個式子，在機器學習中會反覆使用到。

有了期望值的概念，我們開始來看Mean和Variance的定義

Mean的定義為

$$ E[x]\equiv\int^{\infty}_{-\infty}x\cdot p(x)dx \ \ ↪︎【5】 $$

也就是求物理量 $x$ 的期望值。

Variance的定義為

$$ Var[x]\equiv E[(x-E[x])^2] \ \ ↪︎【6】 $$

將上式化約可得

$$ Var[x]=E[x^2]-E[x]^2 \ \ ↪︎【7】 $$

其中：$E[x^2]\equiv\int^{\infty}_{-\infty}x^2p(x)dx$。

接下來只要把式【1】的Normal Distribution代入就可以得到它的Mean和Variance。

在這之前，我們先來看一個重要的積分式：

$$ \int^{\infty}_{-\infty}exp\{-a(x+b)^2\}dx=\sqrt{\frac{\pi}{a}} \ \ ↪︎【8】 $$

上述式子證明稍嫌複雜，有興趣的詳見維基百科的證明。

先看看Normal Distribution是不是機率總和為1

將式【1】做積分

$$ \int^{\infty}_{-\infty}p_{normal}(x)dx=\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}exp\{{-\frac{1}{2\sigma^2}(x-\mu)^2}\}dx $$

接下來令$a=\frac{1}{2\sigma^2}$、$b=-\mu$，此時可以套用式【8】，得

$$ \int^{\infty}_{-\infty}p_{normal}(x)dx=\frac{1}{\sqrt{2\pi}\sigma}\sqrt{\frac{\pi}{\frac{1}{2\sigma^2}}}=1 \ \ ↪︎【9】 $$

再來求其Mean

$$ E_{x\sim normal}[x]=\int^{\infty}_{-\infty}x\cdot p_{normal}(x)dx=\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}x\cdot exp\{{-\frac{1}{2\sigma^2}(x-\mu)^2}\}dx $$

令$s=x-\mu$ 代入上式，得

$$ =\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}(s+\mu)\cdot exp\{{-\frac{1}{2\sigma^2}s^2}\}ds $$

$$ =\frac{1}{\sqrt{2\pi}\sigma}[\int^{\infty}_{-\infty}s\cdot exp\{{-\frac{1}{2\sigma^2}s^2}\}ds+\int^{\infty}_{-\infty}\mu\cdot exp\{{-\frac{1}{2\sigma^2}s^2}\}ds] $$

上式的第一項必為0，因為$s$對原點為奇對稱，而$exp\{{-\frac{1}{2\sigma^2}s^2}\}$對原點為偶對稱，所以$s\cdot exp\{{-\frac{1}{2\sigma^2}s^2}\}$為奇對稱，積分後會相互抵銷為0。接下來把第二項的$s$還原回去，得

$$ =\mu\int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\sigma}exp\{{-\frac{1}{2\sigma^2}(x-\mu)^2}\}dx=\mu \int^{\infty}_{-\infty}p_{normal}(x)dx $$

將式【9】代入，最後得到

$$ E_{x\sim normal}[x]=\mu \ \ ↪︎【10】 $$

最後來算一下Variance

$$ Var_{x\sim normal}[x]=E_{x\sim normal}[x^2]-E_{x\sim normal}[x]^2 \ \ ↪︎【11】 $$

第一項

$$ E_{x\sim normal}[x^2]=\int^{\infty}_{-\infty}x^2p_{normal}(x)dx=\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}x^2\cdot exp\{{-\frac{1}{2\sigma^2}(x-\mu)^2}\}dx $$

令$a=\frac{1}{2\sigma^2}$、$s=x -\mu$

$$ =\sqrt{\frac{a}{\pi}}\int^{\infty}_{-\infty}(s+\mu)^2\cdot exp\{{-a \cdot s^2}\}ds $$

展開

$$ =\sqrt{\frac{a}{\pi}}[\int^{\infty}_{-\infty}s^2\cdot exp\{{-a \cdot s^2}\}ds+\int^{\infty}_{-\infty}2s\mu\cdot exp\{{-a \cdot s^2}\}ds+\int^{\infty}_{-\infty}\mu^2\cdot exp\{{-a \cdot s^2}\}ds] $$

第二項的積分裡面是奇函數，所以第二項積分完的結果是0。第三項把$\mu^2$提出去，積分的部分其實就是式【9】。得

$$ E_{x\sim normal}[x^2]=\sqrt{\frac{a}{\pi}}\int^{\infty}_{-\infty}s^2\cdot exp\{{-a \cdot s^2}\}ds+\mu^2 $$

接下來有點tricky，上式的第一項可看成一個微分形式

$$ =\sqrt{\frac{a}{\pi}}\frac{-\partial}{\partial a}(\int^{\infty}_{-\infty} exp\{{-a \cdot s^2}\}ds)+\mu^2=\sqrt{\frac{a}{\pi}}\frac{-\partial}{\partial a}(\sqrt{\frac{\pi}{a}})+\mu^2=\frac{1}{2a}+\mu^2 $$

所以

$$ E_{x\sim normal}[x^2]=\sigma^2+\mu^2 \ \ ↪︎【12】 $$

將【12】和【10】代入【11】，可得

$$ Var_{x\sim normal}[x]=\sigma^2+\mu^2-(\mu)^2=\sigma^2 \ \ ↪︎【13】 $$

所以未來當你看到Normal Distribution的公式時，應該能夠馬上看出他的Mean和Variance。

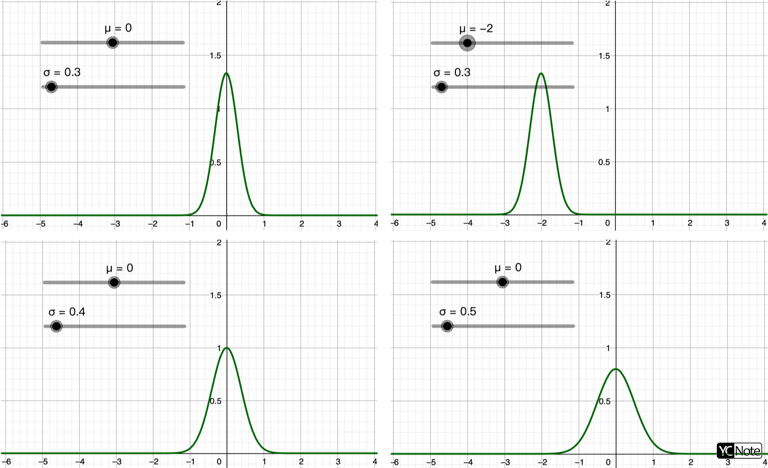
隨機誤差大都呈現Normal Distribution

雖然說並非所有的隨機分布都是Normal Distribution。例如有：適用於二元系統的Bernoulli Distribution；適用於計數系統的Poisson Distribution；適用於時間間隔的Gamma Distribution；...等等。

但是大多數情況下，沒有特別的理由，隨機誤差會遵循Normal Distribution。

接下來我要試著用中央極限定理來解釋這個現象。

先從中央極限定理（Central Limit Theorm）開始講起

Central Limit Theorm:

Let $\{x_1,x_2,...,x_n\}$ be a random sample of size $n$ — that is, a sequence of independent and identically distributed (i.i.d.) random variables drawn from a distribution of expected value $E[x_i]=\mu$ and variance $Var[x_i]=\sigma^2<\infty$. Suppose we are interested in the sample average: $S_n=(x_1+x_2+...+x_n)/n$ , Then as $n\rightarrow \infty$ , $S_n$ follows normal distribution $p_{normal}(\mu,(\frac{\sigma}{\sqrt{n}})^2)$.

也就是說，今天我們從一個任意分布 $p(x)$ 當中採樣 $n$ 筆，這$n$筆採樣的過程符合不互相影響彼此（independent）且都從同一分布而來（identically distributed），即 i.i.d.。

而如果我們已知這個任意分布 $p(x)$ 的Mean $E_{x\sim p(x)}[x]=\mu$ 和 Variance $Var_{x\sim p(x)}[x]=\sigma^2<\infty$，注意：$p(x)$ 不一定需要是Normal Distribution才能算Mean和Variance。

我們關注這$n$筆採樣的平均值，計作$S_n$，統計學告訴我們：

$$ E[S_n]=\mu \ \ ↪︎【14】 $$

$$ Var[S_n]=\frac{\sigma^2}{n} \ \ ↪︎【15】 $$

當$n=1$時，$S_n$的分布其實就是 $p(x)$ 的分布，當然Mean和Variance會和原分布 $p(x)$ 一模一樣。

中央極限定理告訴我們如果今天採樣數量 $n$ 增加到一定的量，$S_n$的分布會趨近於Normal Distribution，也就是說隨著 $n$ 的增加，$S_n$ 的分布會從 $p(x)$ 變成接近 $p_{normal}(\mu,(\frac{\sigma}{\sqrt{n}})^2)$ 分布。

眼見為憑，接下來我要透過Seeing-Theory這個網站來Demo一下中央極限定理，

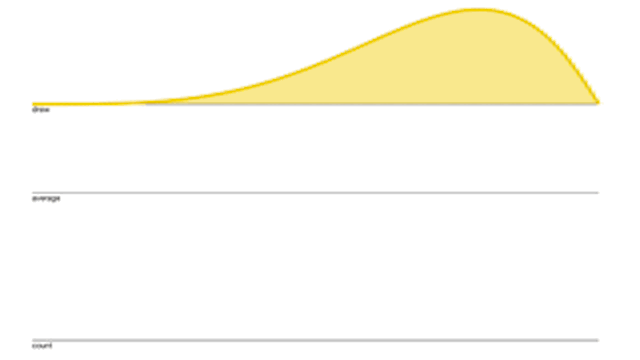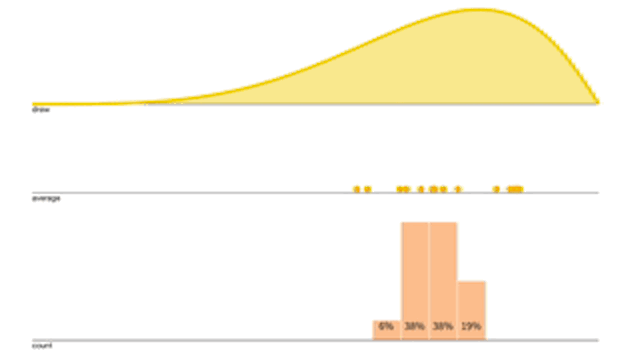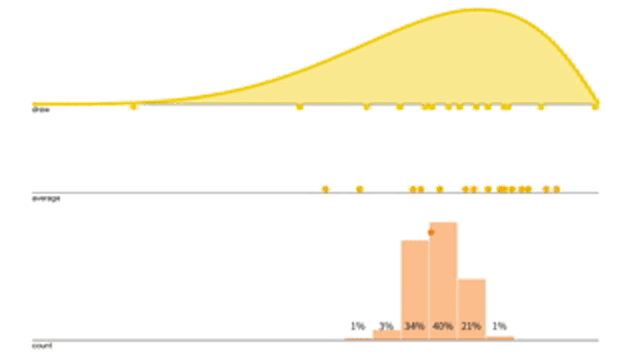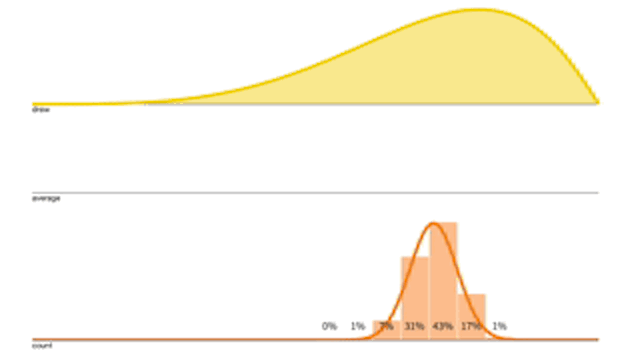
給定一個採樣分布（黃色），每次採樣 $n=15$ 作平均並打點記下來，經過多次的操作就可以得到累積分布圖（紅色），而因為 $n$ 夠大，所以這個累積分布圖會逼近於Normal Distribution。

再來看看採樣平均的累積分布怎麼隨著 $n$ 增加而改變

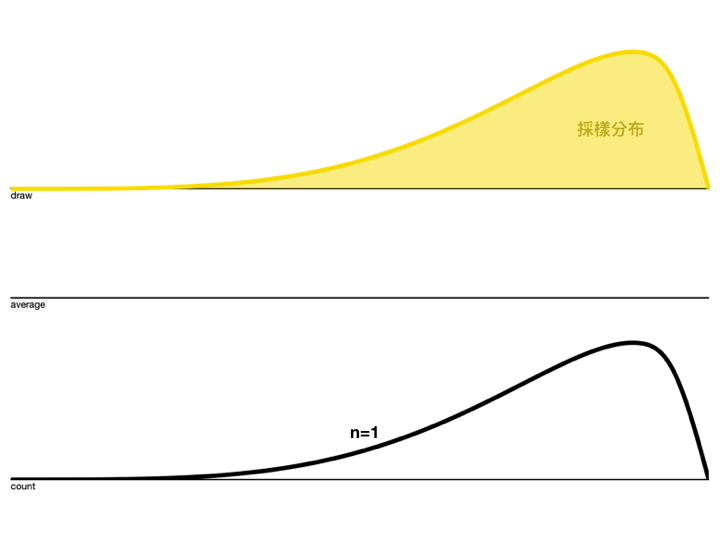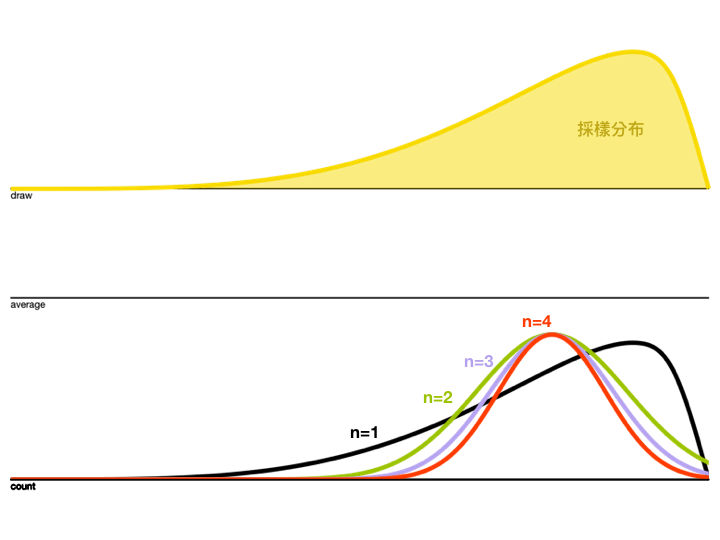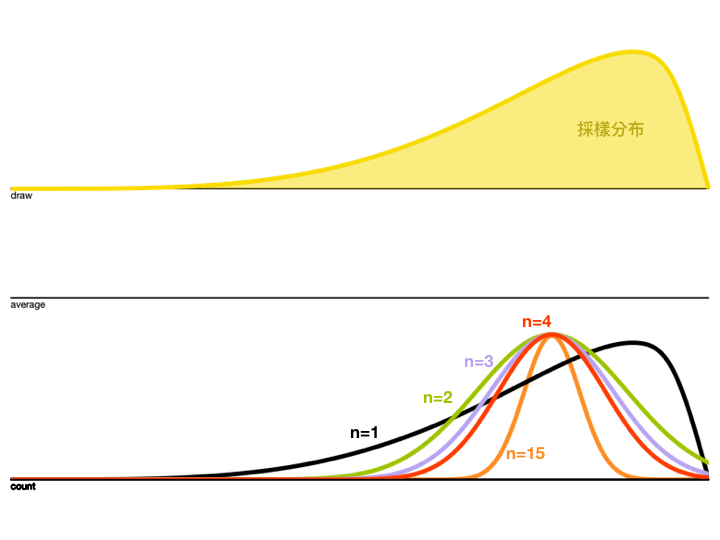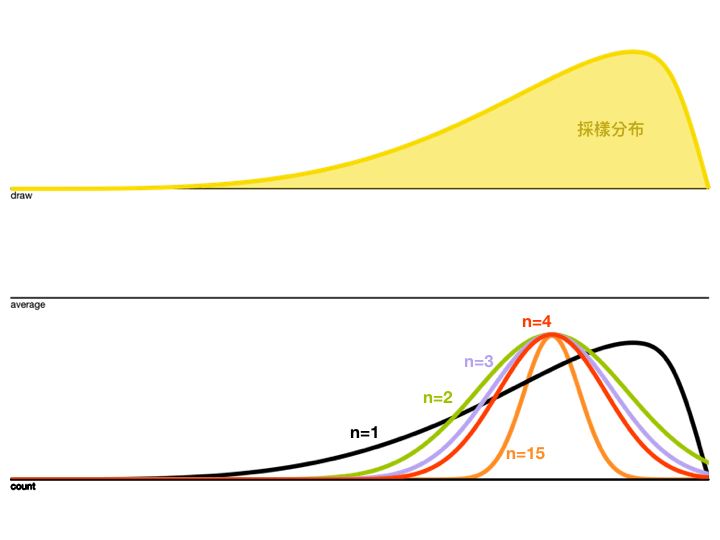
觀察上面的動圖，會發現 $n$ 越大，Variance越來越小，而且分布狀況也越接近Normal Distribution。

好！講了這麼多，那這跟隨機誤差有什麼關係呢？

中央極限定理告訴我們只要從一個固定的採樣分布當中作夠多的樣本平均，其分布會接近Normal Distribution。

而自然界的巨觀現象往往是源自於微觀現象的累積，我們量測的物理量常常來自於多個微小貢獻疊加而成，而不管這些微小貢獻本身的分布狀況如何，其巨觀的物理量因為中央極限定理而成為Normal Distribution，這也是為什麼「隨機誤差大都呈現Normal Distribution」的原因。

舉例，電壓就是反應電荷疊加的物理量，用普通方法我們是很難量到單一電荷的，所以我們能量到的已經是疊加過後的結果，也因此電壓的隨機分布才呈現Normal Distribution。

所以，如果今天你沒有特別的理由，假設Normal Distribution往往是最接近真實的，這是第一個理由能讓你無腦使用Normal Distribution，還有第二個理由我們接下去討論。

Normal Distribution是所有機率分布當中假設最少的

首先來看一段從Goodfellow的書中的一段話，這段話清楚的告訴我們選擇用Normal Distribution的理由

First, many distributions we wish to model are truly close to being normal distributions. The central limit theorem shows that the sum of many independent random variables is approximately normally distributed. This means that in practice, many complicated systems can be modeled successfully as normally distributed noise, even if the system can be decomposed into parts with more structured behavior.

Second, out of all possible probability distributions with the same variance, the normal distribution encodes the maximum amount of uncertainty over the real numbers. We can thus think of the normal distribution as being the one that inserts the least amount of prior knowledge into a model.

-- from: Deep Learning 3.9.3

上述的第一段就是剛剛我們討論的那些，而我們接下去要討論的就是第二段的內容。

總結一下Goodfellow在第二段說的內容：

在所有有相同Variance的分布當中，

Normal Distribution是隨機性最大的分布
Normal Distribution是最少先驗知識（Prior Knowledge）假設的

要討論這個問題，我們必須先了解一些資訊理論。

在資訊理論當中，我們常常使用Entropy（熵）來衡量隨機性，Entropy的定義為

$$ H\equiv E[-ln\ p(x)] \ \ ↪︎【16】 $$

因為篇幅的緣故，Entropy的完整介紹會在接下來的文章中介紹，請大家先把這個定義背起來。

透過式【2】可以將Entropy寫成連續形式：

$$ H_{x\sim p(x)}=E[-ln\ p(x)]=- \int^{\infty}_{-\infty}ln\ p(x)\cdot p(x)dx \ \ ↪︎【17】 $$

接下來將Normal Distribution 【1】式代入【17】

$$ H_{x\sim normal}=- \int^{\infty}_{-\infty}p_{normal}(x)\cdot ln\ p_{normal}(x) dx $$

$$ =- \int^{\infty}_{-\infty}\frac{1}{\sqrt{2\pi}\sigma}exp\{{-\frac{1}{2\sigma^2}(x-\mu)^2}\} \cdot [ln(\frac{1}{\sqrt{2\pi}\sigma})-\frac{1}{2\sigma^2}(x-\mu)^2]dx $$

$$ =ln(\sqrt{2\pi}\sigma)+ \frac{1}{2\sigma^2} \int^{\infty}_{-\infty}\frac{1}{\sqrt{2\pi}\sigma}exp\{{-\frac{1}{2\sigma^2}(x-\mu)^2}\} \cdot (x-\mu)^2dx $$

$$ =ln(\sqrt{2\pi}\sigma)+ \frac{1}{2\sigma^2} E_{x\sim normal}[(x-\mu)^2] $$

$$ =ln(\sqrt{2\pi}\sigma)+ \frac{1}{2\sigma^2} Var_{x\sim normal}[x] $$

$$ H_{x\sim normal}=ln(\sqrt{2\pi}\sigma)+\frac{1}{2}=\frac{1}{2}ln(2\pi e\sigma^2) \ \ ↪︎【18】 $$

我們因此得到了Normal Distribution 的Entropy，而這個Entropy是所有有相同Variance的分布當中最大的。緊接著來證明這件事。

回到式【17】，我們可以列出一個有限制條件的優化問題：

在給定：

$\int p(x)dx=1 \ \ ↪︎【19】$
$E[x]=\mu \ \ ↪︎【20】$
$Var[x]=\sigma^2 \ \ ↪︎【21】$

的情況下試圖找到一個 $p(x)$ 可以使 Entropy $H$ 最大：

$$ p^*(x) = argmax_{p(x)}\ H_{x\sim p(x)}=argmin_{p(x)}\int^{\infty}_{-\infty}ln\ p(x)\cdot p(x)dx \ \ ↪︎【22】 $$

引入Lagrange Multiplier結合【19】,【20】,【21】,【22】：

$$ L=\int^{\infty}_{-\infty}ln\ p(x)\cdot p(x)dx-\lambda_1 (\int^{\infty}_{-\infty}p(x)dx-1)-\lambda_2(\int^{\infty}_{-\infty}x\cdot p(x)dx-\mu)-\lambda_3(\int^{\infty}_{-\infty}(x-\mu)^2\cdot p(x)dx-\sigma^2) $$

$$ =\int^{\infty}_{-\infty}[-\lambda_1 p(x)-\lambda_2 p(x)x-\lambda_3 p(x)(x-\mu)^2+p(x)ln(p(x))]dx+\lambda_1 +\mu\lambda_2+\sigma^2\lambda_3 \ \ ↪︎【23】 $$

接下來對【23】微分求極值

$$ 0=\frac{\partial L}{\partial p(x)}|_{p^*(x)}=\int^{\infty}_{-\infty}[-\lambda_1-\lambda_2 x-\lambda_3 (x-\mu)^2+ln(p^*(x))+1]dx \ \ ↪︎【24】 $$

所以

$$ p^*(x)=exp\{\lambda_1+\lambda_2 x+\lambda_3 (x-\mu)^2-1\} \ \ ↪︎【25】 $$

上面還有三個未知變數 $\lambda_1$, $\lambda_2$, $\lambda_3$ ，這些變數必須滿足Constraints，所以將【25】代入【19】,【20】,【21】得三個方程求解三個變數，可得：

$$ \lambda_1=1-ln(\sqrt{2\pi}\sigma);\ \lambda_2=0;\ \lambda_3=-\frac{1}{2\sigma^2} \ \ ↪︎【26】 $$

最後將【26】回代【25】就會得到剛剛好是Normal Distribution，🥳

因此這邊我們證明了：在給定Mean和Variance下，Normal Distribution為所有分布當中Entropy最大的。這也同時意味著，Normal Distribution是隨機性最大的，Normal Distribution是額外假設最少的。

Back to the Question

這一講也走到尾聲了，接下來我們已經有能力回答一開始問的問題，在回答問題之前我們複習一下剛剛學到了什麼。

中央極限定理告訴我們：如果今天採樣數量 $n$ 增加到一定的量，$S_n$的分布會趨近於Normal Distribution
自然界的巨觀現象往往是源自於微觀現象的累積，我們量測的物理量常常來自於多個微小貢獻疊加而成，而不管這些微小貢獻本身的分布狀況如何，其巨觀的物理量因為中央極限定理而成為Normal Distribution，這也是為什麼「隨機誤差大都呈現Normal Distribution」的原因
Entropy是衡量隨機性的指標，定義為：$H\equiv E[-ln\ p(x)]$
在給定Mean和Variance下，Normal Distribution為所有分布當中Entropy最大的。這也同時意味著，Normal Distribution是隨機性最大的，Normal Distribution是額外假設最少的

因此我們有兩個原因去使用Normal Distribution

如果沒有特別理由，請假設隨機誤差為Normal Distribution，因為自然界的隨機誤差大都呈現Normal Distribution
如果想要人為假設一個分布，請優先選擇Normal Distribution，因為它是包含最少先驗知識（Prior Knowledge）的分布

最後來逐一回答剛開始的問題

Q：為什麼Normal Distribution通常作為雜訊的分布？
- A：因為自然界的隨機誤差大都呈現Normal Distribution
Q：為何在DL（deep learning），參數的初始化要用Normal Distribution？
- A：因為它是包含最少先驗知識（Prior Knowledge）的分布
Q：為何在Bayesian公式裡常常會使用Normal Distribution當作Prior Probability？
- A：因為它是包含最少先驗知識（Prior Knowledge）的分布
Q：在使用GAN（generative adversarial network）時，為什麼給予的輸入要假設Normal Distribution？
- A：因為它是包含最少先驗知識（Prior Knowledge）的分布

Reference

Seeing Theory
Ian Goodfellow and Yoshua Bengio and Aaron Courville. Deep Learning. 2016.
Christopher Bishop. Pattern Recognition and Machine Learning. 2006.

[此文章為原創文章，轉載前請註明文章來源]

Previous Post Next Post