剖析深度學習 (2)：你知道Cross Entropy和KL Divergence代表什麼意義嗎？談機器學習裡的資訊理論

Posted on February 25, 2020 in AI.ML. View: 41,426

深度學習發展至今已經有相當多好用的套件，使得進入的門檻大大的降低，因此如果想要快速的實作一些深度學習或機器學習，通常是幾行程式碼可以解決的事。但是，如果想要將深度學習或機器學習當作一份工作，深入了解它背後的原理和數學是必要的，才有可能因地制宜的靈活運用，YC準備在這一系列當中帶大家深入剖析深度學習。

在上一講當中，我鉅細靡遺的介紹了Normal Distribution。其中我有稍微的提到Entropy的概念，並且說在未來會有一講專門來談機器學習裡面會用到的資訊理論，而那個未來就是現在！

在深度學習裡面，尤其是分類問題，常常會用到Cross Entropy，教學上通常會從Maximum Likelihood推導而來，但是Cross Entropy其實具有更廣義的涵義，甚至不限於分類問題使用。

還有學習過程也經常會出現KL Divergence這樣既熟悉又陌生的東西，甚至到了GAN會用到更多種類的Divergence，例如：JS Divergence。

這全部都與資訊理論息息相關，這一講讓我們來搞清楚Entropy、Cross Entropy、KL Divergence和f-Divergence到底具有什麼涵義。

這一切都要先從Entropy開始講起。

資訊熵（Information Entropy）

資訊理論是應用數學的一個分支，主要是對訊號中存在的資訊多寡做量化。最初研究目的是為了數據傳輸的編碼，探討要怎麼編碼資料傳輸才有效率。

資訊理論背後的直覺是，越是不容易發生的事件帶給我們的資訊量越大，資訊量的大小可以看作是事件給我們的驚訝程度。舉個例子，「今天早上太陽升起」這樣幾乎永遠都是對的事件，能帶給我們的資訊量可以說是零（你不用告訴我，我也知道）；相反的「今天早上有日蝕」的事件則含有相對多的資訊量。

$事件的資訊量 \propto 事件的不確定程度$

有了這樣的洞見，我們怎麼把它化成數學呢？我們可以定義事件的Self-Information為：

$$ I(x)=-log_2p(x) \ \ ↪︎【1】 $$

其中$log_2$以2為底，則代表所採用的單位為 bits (比特)；$p(x)$代表的是事件的出現機率，此式子符合以下四個特性

當$0<p(x)\leq 1$時，則$I(x)>0$，這意味著資訊量必為正，如果遇到雜訊干擾才有可能扣掉一些資訊量
當事件永遠是對的時，則$p(x)=1$，相應的 $I(x)=0$，代表資訊量為零
當$p(x)$越小，則$I(x)$越大，意味著事件出現的機率越小，它所攜帶的資訊量越大
若$p(x)=p_1(x)\times p_2(x)$則代表兩個獨立事件發生的機率是相乘的關係，此時資訊量應該是相加的關係，關係式$I(x)=I_1(x)+I_2(x)$正表示這樣的關係

Self-Information只處理單一結果，我們更想要關注整個系統，Shannon Entropy可以量化整個機率分布中不確定性的程度：

$$ H(x)=E_{x\sim p}[I(x)]=-E_{x\sim p}[log_2p(x)] \ \ ↪︎【2】 $$

上式所傳達的意思是：Shannon Entropy即是評估Self-Information的期望值。

為了進一步的了解Shannon Entropy的內涵，我們來舉個例子。假設你的系統是離散的，可以進一步表示成為

$$ H(x)=-E_{x\sim p}[log_2p(x)]=-\sum_i p_ilog_2 p_i \ \ ↪︎【3】 $$

假設你要描述的事件有三個獨立事件A、B和C，A事件出現機率為$1/2$，B事件出現機率為$1/4$，C事件出現機率為$1/4$，代入式【3】求系統的Shannon Entropy：

$$ H=-\frac{1}{2}log_2(\frac{1}{2})-\frac{1}{4}log_2(\frac{1}{4})-\frac{1}{4}log_2(\frac{1}{4})=0.5+0.5+0.5=1.5 \ \ ↪︎【4】 $$

這代表什麼意義呢？這代表今天如果你設計一個系統得當的話，你只需要用到平均1.5個bits來傳輸。怎麼說呢？我們逐步拆解式【4】帶給我們的觀念：

A事件的$I=1$，代表用1個bit去傳輸A事件，即$bits_A=1$，可能編碼為0
B事件的$I=2$，代表用2個bits去傳輸B事件，即$bits_B=2$，可能編碼為10
C事件的$I=2$，代表用2個bits去傳輸C事件，即$bits_C=2$，可能編碼為11

你會發現經常出現的事件A就用較少的bits來傳輸，而較不常發生的事件B就用比較多的bits來傳輸，如此一來傳輸會更有效率。假設有200個事件要傳輸，依照機率分布，其中應該有100件屬於A事件，有50件屬於B事件，有50件屬於C事件，依照上述的編碼方式，我們傳輸這200個事件所需要的預期平均bits數就是1.5。

$$ \frac{n_A\times bits_A+n_B\times bits_B+n_C\times bits_C}{n_A+n_B+n_C}=\frac{100\times 1+50\times 2+50\times 2}{200}=1.5 \ \ ↪︎【5】 $$

而理論告訴我們這 $1.5$ 其實就是最小的預期位元，你無法找到比這個更小的，也就是說：你無法找到比這個更有效率的編碼系統。理論如下：

The Noiseless Coding Theorm (Shannon, 1948):

The entropy is a lower bound on the number of bits needed to transmit the state of a random variable.

來做個小結論，仔細回想剛剛的過程你會更能了解公式隱藏的意義。如果你仔細的去理解剛剛我舉的例子，你會發現： $I(x)$，或者Entropy中的$-log$ ，所扮演的角色是「編碼」，決定需要用幾個bits來傳輸事件，而Entropy的意義就是這套「編碼」運用到系統的bits期望值，並且Shannon的理論告訴我們$-log\ p(x)$已經是最有效率的「編碼」，它可以得到最小的bits期望值，所以Entropy是bits期望值的下界。

在物理上或是機器學習上，我們常使用自然對數$e$當作底，所以Entropy為：

$$ H(p)=E_{x\sim p}[-\operatorname{ln}p(x)] \ \ ↪︎【6】 $$

其實就只是把度量的單位從比特(bits)換成奈特(nats)，只是「編碼」的單位改變而已，其意義都跟上述的一樣。只是如果使用nats當單位在計算上會方便許多，因為許多的分布都可以表示成以$e$為底的指數，例如：Normal Distribution。

還記得上一講中我請大家記住的【2】到【4】式嗎？現在套用到這裡的【6】，可得：

連續情境下， $H=\int -p(x)\operatorname{ln}p(x)dx \ \ ↪︎【7】$
離散情境下， $H=\sum_i -p_i\operatorname{ln}p_i \ \ ↪︎【8】$
實驗情境下，$H=\sum_k -(\frac{n_k}{N})\operatorname{ln}(\frac{n_k}{N}) \ \ ↪︎【9】$

最後，來看看什麼分布的Entropy最大，在給定 $\int p(x)dx=1$ 的情況下試圖找到一個 $p(x)$ 可以使 Entropy $H$ 最大，引入Lagrange Multiplier：

$$ L=\int^{\infty}_{-\infty}-\operatorname{ln}p(x)\cdot p(x)dx+\lambda (\int^{\infty}_{-\infty}p(x)dx-1) $$

$$ =\int^{\infty}_{-\infty}[\lambda p(x)-p(x)\operatorname{ln}(p(x))]dx-\lambda \ \ ↪︎【11】 $$

接下來對【11】微分求極值

$$ 0=\frac{\partial L}{\partial p(x)}|_{p^*(x)}=\int^{\infty}_{-\infty}[\lambda-\operatorname{ln}(p^*(x))-1]dx \ \ ↪︎【12】 $$

所以

$$ p^*(x)=exp\{\lambda-1\} \ \ ↪︎【13】 $$

此時的分布是一個與 $x$ 無關的常數，所以 $p^*(x)$ 是一個Uniform Distribution。所以平均分配會使得系統得到最大的Entropy，也就是Uniform Distribution是隨機性最大的分布，也是資訊量最大的分布 ，這與我們剛剛的討論是自恰的。（注意：在有限Variance的情況下是Normal Distribution有最大Entropy）

Cross Entropy

接下來聊聊學過機器學習和深度學習都知道的Cross Entropy，在分類問題當中Cross Entropy被定義成：

$$ Cross\ Entropy=-y\ \operatorname{ln}(q)-(1-y)\operatorname{ln}(1-q) \ \ ↪︎【14】 $$

其中：$y_i=0,1$為data的labels，$q_i$為模型預測的輸出值。

但它其實有更一般的定義：

$$ Cross\ Entropy:\ H(p, q)=E_{x\sim p}[-\operatorname{ln}q(x)] \ \ ↪︎【15】 $$

一般$p(x)$代表的是目標分布，也就是想要學習的未知分布；而$q(x)$則代表是模型的輸出分布。

我們剛剛說過Entropy是bits或nats期望值的下界，所以：

$$ H(p,q)=E_{x\sim p}[-\operatorname{ln}q(x)]\geq E_{x\sim p}[-\operatorname{ln}p(x)]=H(p,p)=H(p) \ \ ↪︎【16】 $$

所以當我們試圖減少Cross Entropy時，其實就是試圖調整$q(x)$使其接近$p(x)$，因為當$q(x)=p(x)$時，$H(p,q)=H(p)$有最小的Cross Entropy。

延續剛剛「編碼」的概念套用在Cross Entropy，今天我雖然知道 $-\operatorname{ln}p(x)$是最好的「編碼」，但是我不知道 $p(x)$ 長什麼樣子，所以退一步我們使用模型的 $q(x)$ 來做「編碼」，Cross Entropy的意義就是利用 $-\operatorname{ln}q(x)$ 這套「編碼」去算系統的nats期望值，並且想辦法改善編碼方法來降低Cross Entropy。

接下來我想要帶大家從式【15】到【14】導一遍式子。

因為我們知道目標分布是Binary的離散系統，所以可以把【15】寫成：

$$ H(p,q)=-p_{positive}\cdot \operatorname{ln}(q_{positive})-p_{negative}\cdot \operatorname{ln}(q_{negative}) \ \ ↪︎【17】 $$

因為是Binary Classification的問題，只有兩種states其機率相合為1，因此：

$$ H(p,q)=-p_{positive}\cdot \operatorname{ln}(q_{positive})-(1-p_{positive})\cdot \operatorname{ln}(1-q_{positive}) \ \ ↪︎【18】 $$

接下來，$p$ 是目標分布，當label為positive ($y=1$) 則$p_{positive}=1$，當label為 ($y=0$) negative則$p_{positive}=0$；$q$ 是模型預測，其目標是預測positive的可能機率，所以最後寫成：

$$ H(p,q)=-y\cdot \operatorname{ln}(q)-(1-y)\cdot \operatorname{ln}(1-q) $$

就跟【14】式一模一樣了，這裡注意一點，在推導的過程當中我都不需要去假設模型的長相，我不需要假設模型為Sigmoid，推出Cross Entropy的過程是和模型的選擇無關的，所以千萬不要認為選擇使用Cross Entropy是因為Sigmoid的緣故。進一步說Cross Entropy其實可以用在各種問題（或分布），包括：Regression問題，我們會在接下來的文章裡讓大家真正了解這一點。

KL Divergence (Kullback-Leibler Divergence)

KL Divergence對碰過深度學習一段時間的大家應該是一個既熟悉又陌生的東西吧！我們就在這邊把它搞懂吧！

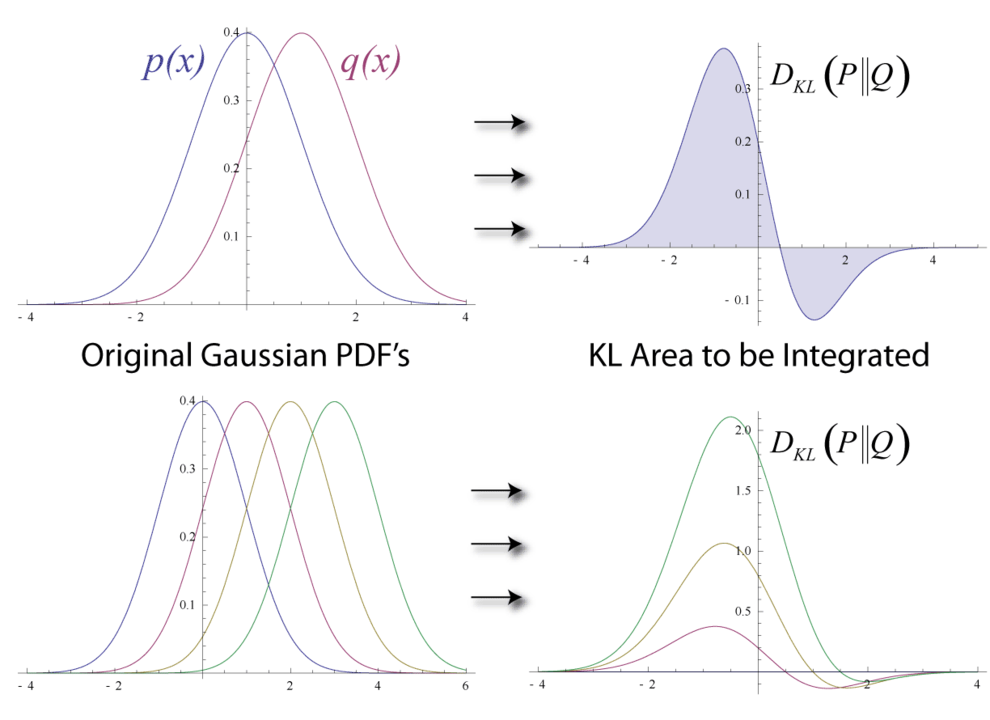
如果有兩個獨立的機率分布$p(x)$和$q(x)$同時對應到同一個隨機變數$x$，也就是它們所在的空間是一樣的，則可以使用KL Divergence來測量這兩個分布的差異程度：

$$ D_{KL}(p||q)=-E_{x\sim p}[\operatorname{ln}q(x)-\operatorname{ln}p(x)]=-E_{x\sim p}[\operatorname{ln}\frac{q(x)}{p(x)}] \ \ ↪︎【19】 $$

這個式子不好懂，沒關係！我們稍微代換一下式子：

$$ D_{KL}(p||q)=E_{x\sim p}[-\operatorname{ln}q(x)]-E_{x\sim p}[-\operatorname{ln}p(x)]=H(p,q)-H(p) \ \ ↪︎【20】 $$

有看出來了嗎？KL Divergence其實就是Cross Entropy扣掉目標分布的Entropy，更深層的說，KL Divergence表示的是目前的編碼方法最多還可以下降多少nats期望值。

雖然你可以將KL Divergence視作距離，但是嚴格來說它不是，因為KL Divergence不具有對稱性：

$$ D_{KL}(p||q)\neq D_{KL}(q||p) \ \ ↪︎【21】 $$

其中：

$$ D_{KL}(q||p)＝-E_{x\sim q}[\operatorname{ln}p(x)-\operatorname{ln}q(x)]＝H(q,p)-H(q) \ \ ↪︎【22】 $$

【21】式意味著從$p(x)$到$q(x)$所降低的nats期望值與從$q(x)$到$p(x)$所降低的nats期望值不相等。

f-Divergence

Divergence其實有多個形式，定義如下：當有兩個獨立的機率分布$p(x)$和$q(x)$同時對應到同一個隨機變數$x$，

$$ f-divergence:\ D_f(p\|q)=E_{x\sim q}[f(\frac{p(x)}{q(x)})]=\int q(x)f(\frac{p(x)}{q(x)})dx $$

其中：$f(.)$ 只需要遵守兩條規則就可以：$f(.)$ 是Convex的且$f(1)=0$。

當$f(u)=u\cdot \operatorname{ln}u$，則
$$ D_f(p\|q)=\int q(x)(\frac{p(x)}{q(x)})\operatorname{ln}(\frac{p(x)}{q(x)})dx=\int p(x)\operatorname{ln}(\frac{p(x)}{q(x)})dx=D_{KL}(p\|q) $$
，為KL Divergence
當$f(u)=-\operatorname{ln}u$，則
$$ D_f(p\|q)=-\int q(x)\operatorname{ln}(\frac{p(x)}{q(x)})dx=\int q(x)\operatorname{ln}(\frac{q(x)}{p(x)})dx=D_{KL}(q\|p) $$
，為Reverse KL Divergence
當$f(u)=(u-1)^2$，則
$$ D_f(p\|q)=-\int q(x)(\frac{p(x)}{q(x)}-1)^2dx=\int \frac{(p(x)-q(x))^2}{q(x)}dx $$
，為Chi Square Divergence
當$f(u)=-(u+1)\operatorname{ln}\frac{u+1}{2}+u\operatorname{ln}u$，則
$$ D_f(p\|q)=\frac{1}{2}[D_{KL}(p\|\frac{p+q}{2})+D_{KL}(q\|\frac{p+q}{2})] $$
，為 JS Divergence (用在GAN)

f-divergence在意義上代表：我在model的分布 $q(x)$ 上估計 $f(\frac{p(x)}{q(x)})$ ，$f(.)$是用來評估分布間距離的函數，當$p(x)=q(x)$時距離為0 — $f(\frac{p(x)}{q(x)})=0$，當$p(x)\neq q(x)$時距離為正 — $f(\frac{p(x)}{q(x)})> 0$。

結論

機器學習和深度學習充分的借用了資訊理論裡對資訊量的衡量技術，包括：Entropy、Cross Entropy和KL Divergence。因為機器學習中充斥著統計分布，而這些衡量方法可以幫助我們度量種種分布的資訊量，有了這把尺我們才可以進行各類優化來讓機器學習。

Entropy: $H(p)=E_{x\sim p}[-\operatorname{ln}p(x)]$ ，為最小可得的nats期望值
Cross Entropy: $H(p, q)=E_{x\sim p}[-\operatorname{ln}q(x)]$ ，利用$q(x)$來編碼可得的nats期望值
KL Divergence: $D_{KL}(p\|q)=H(p,q)-H(p)$ ，表示的是目前的編碼方法最多還可以下降多少nats期望值

其實，這一講的內容可以說是為了接下來幾講而生，下一講我們會開始套用資訊理論的這些概念，帶大家重新了解優化和擬合是怎麼一回事，敬請期待！

Reference

Ian Goodfellow and Yoshua Bengio and Aaron Courville. Deep Learning. 2016.
Christopher Bishop. Pattern Recognition and Machine Learning. 2006.
Wiki: Entropy_(information_theory)
Wiki: Cross Entropy
Wiki: Kullback–Leibler_divergence
從計算機編碼的角度看Entropy
李宏毅, GAN Lecture 5 (2018): General Framework

[此文章為原創文章，轉載前請註明文章來源]

Previous Post Next Post

資訊熵（Information Entropy）

Cross Entropy

KL Divergence (Kullback-Leibler Divergence)

f-Divergence

結論

Reference

Part 2 of the "剖析深度學習" series

Previous articles

Next articles