剖析深度學習 (3)：MLE、MAP差在哪？談機器學習裡的兩大統計觀點

Posted on March 07, 2020 in AI.ML. View: 20,559

剖析深度學習

深度學習發展至今已經有相當多好用的套件，使得進入的門檻大大的降低，因此如果想要快速的實作一些深度學習或機器學習，通常是幾行程式碼可以解決的事。但是，如果想要將深度學習或機器學習當作一份工作，深入了解它背後的原理和數學是必要的，才有可能因地制宜的靈活運用，YC準備在這一系列當中帶大家深入剖析深度學習。

本講主要探討統計的兩大學派（頻率學派和貝氏學派）對於機器如何學習的觀點。頻率學派主張Maximum Likelihood Estimation (MLE)，會提到這等同於最小化data與model之間的Cross Entropy或KL Divergence。而貝氏學派則主張Maximum A Posterior (MAP) ，會提到這會等同於極大化Likelihood並同時考慮Regularization Term，我們也可以在本講看到L1和L2 Regularation Term是怎麼被導出的。

條件機率

因為本講會牽涉到許多條件機率的計算，所以把條件機率常用的公式先列下來，讓大家溫習一下。

  • 邊際機率（marginal probability）

    $$ p(X=x_i)=\sum_j p(X=x_i, Y=y_j) \ \ ↪︎【1】 $$
    (如下圖所示)

  • 條件機率（conditional probability）

    $$ p(X=x_i, Y=y_j)=p(Y=y_j\mid X=x_i)p(X=x_i) \ \ ↪︎【2】 $$
    (如下圖所示)

  • 條件機率的鏈鎖法則

    $$ p(a,b,c)=p(a\mid b,c)\cdot p(b,c)=p(a\mid b,c)\cdot p(b\mid c)\cdot p(c) \ \ ↪︎【3】 $$
    (因為 \(a\cap b\cap c=a\cap (b\cap c)\))

  • 獨立性

  • if X and Y are independent, \(p(X=x_i,Y=y_j)=p(X=x_i)\cdot p(Y=y_j)\)

  • if X and Y are independent, \(p(X=x_i,Y=y_j\mid Z=z_k)=p(X=x_i\mid Z=z_k)\cdot p(Y=y_j\mid Z=z_k) \ \ ↪︎【4】\)

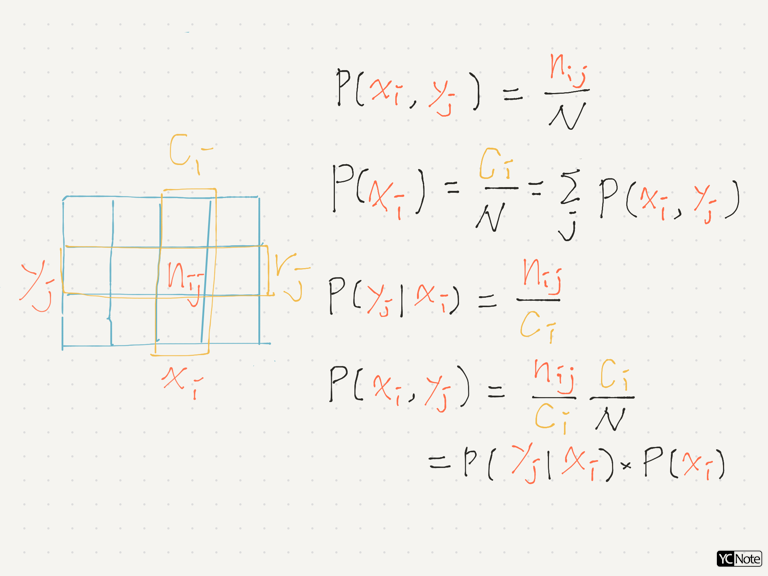
碰到條件機率，心中應該要有這張圖，如果公式忘記了也可以輕易的推出來

頻率學派 v.s. 貝氏學派

頻率學派和貝氏學派為統計上面重要的兩大觀點，透徹的了解這兩個學派的觀點，可以幫助你在做機器學習或深度學習時選擇模型有所幫助。

舉個例子，如果你在做詞性標記（POS tagging）的任務，你採用隱馬爾科夫模型 (HMM)，那麼你採用的是類似貝氏學派的觀點；但如果你採用 Conditional Random Field (CRF)，那麼你就是採用類似頻率學派的觀點。

再舉個平易近人一點的例子，Loss Function中的Regularization Term其實可以看作是從先驗機率 (Prior Probability) 來的，這也有貝氏學派的味道，待會會再仔細的介紹。

簡單講，頻率學派相信世界的本質是穩定的，所有現象背後都有一個穩定的母群體，所以我們只要透過來自母群體大量隨機且可重複實驗的事件，就可以透過期望值估算各種統計量，這就是頻率學派的認知：不需要太多其他的人為假設，只需要單純從母群體抽樣即可。

但是貝氏學派不這麼認為，他們認為至少有一些現象是不穩定的，例如：北極的冰是否會在本世紀溶解殆盡，這種問題不存在穩定的母群體讓你可以在短時間內「大量」的量測，因為系統不斷的在演進，因此我們需要有一個具有演進特性的統計模型，那就是貝氏機率，貝氏機率的精髓是演進，手中先握著一個先驗機率 (Prior Probability) ，再透過不斷觀察新的證據來更新手上的機率。

在機器學習上，頻率學派的優點是無額外的假設，相反的貝氏學派需要假設先驗機率 (Prior Probability) ，錯誤的先驗機率可能會去誤導模型，讓它反而忽視甚至曲解數據帶來的信息。另外，貝氏學派的優點也正是因為它有先驗機率，所以在資料筆數不多的情況下較不容易出錯，如果你使用頻率學派的觀點在小樣本上，由於統計量不足可能導致你的估計也不準確。

所以說，先驗機率的使用是把雙面刃，水可載舟亦可覆舟。

Maximum Likelihood Estimation (MLE)

首先我們來看頻率學派，也就是傳統學派，究竟用什麼什麼觀點讓機器學習的，我們從頭到腳來理一遍。

給定一個Dataset \(\mathcal{D}\) ，並且決定好Model的Hyperparameters \(m\)，此時我只需要尋找Model權重參數 \(\theta\) ，就可以決定好一個Model。

那怎麼決定 \(\theta\) 呢？頻率學派認為只要先決定好Model (決定\(m\)和\(\theta\))，再算算看這個Model產生Dataset \(\mathcal{D}\) 的機率，這就是Likelihood，我們希望這個Likelihood可以越高越好，也就是Maximum Likelihood。化成數學式子： ⚠️

$$ \theta_{MLE}=argmax_\theta\ p(\mathcal{D}\mid m,\theta) \ \ ↪︎【5】 $$

其中：\(p(\mathcal{D}\mid m,\theta)\) 稱為Likelihood。

而Dataset \(\mathcal{D}\) 理當有多筆資料：

$$ =argmax_\theta\ p_{\mathcal{D}_1,...,\mathcal{D}_N}(d_1,...,d_N\mid m,\theta) \ \ ↪︎【6】 $$

假設從Dataset \(\mathcal{D}\) 抽樣資料的過程每一筆是Independent的，則

$$ =argmax_\theta\ \prod_{i}\ p_{\mathcal{D}_i}(d_i\mid m,\theta) \ \ ↪︎【7】 $$

再假設從Dataset \(\mathcal{D}\) 抽樣資料的過程是從同一個分布來的 (identically distributed) ，則

$$ \theta_{MLE}=argmax_\theta\ \prod_{i}\ p(d_i\mid m,\theta) \ \ ↪︎【8】 $$

接下來，為了方便計算而取 \(\operatorname{ln}\)：

$$ \theta_{MLE}=argmax_\theta\ \sum_{i}\ \operatorname{ln}p(d_i\mid m,\theta) \ \ ↪︎【9】 $$

再來我們考慮監督式學習的情況，每一筆數據 \(d_i\) 是由一對輸入與輸出所組成 \((x_i, y_i)\) ：

$$ \theta_{MLE}=argmax_\theta\ \sum_{i}\ \operatorname{ln}p(x_i,y_i\mid m,\theta) \ \ ↪︎【10】 $$

因為 \(y_i\) 是depend on \(x_i\) 的，所以使用【3】式將 \(x_i\) 往後搬，得

$$ =argmax_\theta\ \sum_{i}\ \operatorname{ln}[p(y_i\mid x_i,m,\theta)p(x_i\mid m,\theta)] \ \ ↪︎【11】 $$

\(x_i\) 與 model參數 \(m\) 和 \(\theta\) 應該是互相獨立的，

$$ =argmax_\theta\ \sum_{i}\ \operatorname{ln}[p(y_i\mid x_i,m,\theta)p(x_i)] \ \ ↪︎【12】 $$
$$ =argmax_\theta\ \sum_{i}\ \operatorname{ln}p(y_i\mid x_i,m,\theta)+\operatorname{ln}p(x_i) \ \ ↪︎【13】 $$

\(p(x_i)\) 與\(\theta\) 無關，在優化過程可忽略，得： ⚠️

$$ \theta_{MLE}=argmax_\theta\ \sum_{i}\ \operatorname{ln}p(y_i\mid x_i,m,\theta) \ \ ↪︎【14】 $$

上面這個式子是可以透過實驗來找到 \(\theta_{MLE}\) 的，其中 \(p(y_i\mid x_i,m,\theta)\) 表示在Model固定的情況下，估計輸入\(x_i\)會得到\(y_i\)的機率，我們可以透過Grandient Descent的方法調整參數來最大化這一項，詳細怎麼做我會在下一講交代清楚。

還沒有結束喔！大家有沒有覺得【14】式怪眼熟的，這很像是我們在上一講討論的東西。

我們把【14】式乘上負號，再除上資料筆數 \(N\)，得

$$ \theta_{MLE}=argmin_\theta\ \frac{1}{N}\sum_{i}-\operatorname{ln}p(y_i\mid x_i,m,\theta) \ \ ↪︎【15】 $$

有沒有看出來！沒有的話，我們繼續導下去，\(\frac{1}{N}\sum_i\) 其實就是代表對data的採樣並平均，將它表示成為期望值

$$ \theta_{MLE}=argmin_\theta\ E_{x\sim p_{data}}[-\operatorname{ln}p_{model}(y_i\mid x_i,m,\theta)]＝argmin_\theta\ H(p_{data},p_{model}) \ \ ↪︎【16】 $$

所以說Maximum Likelihood就是在最小化Data和Model的Cross Entropy，當\(p_{data}=p_{model}\)時有最小的Cross Entropy，這也間接證明了Maximum Likelihood的最優解就是\(p_{data}=p_{model}\)，也就是model分布等同於母體分布。

當然，你也可以說Maximum Likelihood就是在最小化KL Divergence，KL Divergence：

$$ D_{KL}(p_{data}\| p_{model})=E_{x\sim p_{data}}[\operatorname{ln}p_{data}(x)-\operatorname{ln}p_{model}(x)] \ \ ↪︎【17】 $$

但是因為 \(\operatorname{ln}p_{data}(x)\) 與 \(\theta\) 無關，所以計算還是只剩下第二項的Cross Entropy。

特別注意，剛剛的所有推論並沒有提到我們的問題是Regression問題還是Classification問題，再次強調Cross Entropy並不專屬於Sigmoid或Softmax，甚至下一講我還會提到Mean Squared Error是源於Data分布與Normal Distribution的Cross Entropy。

Maximum A Posterior (MAP)

再來我們聊聊貝氏學派，我們好奇頻率學派究竟有什麼不足？MLE有什麼不足？為什麼我們需要一個新的觀點。

最重要的一點是MLE認為所有 \(\theta\) 出現的機率是均等的，我們優化的目標是 \(p(\mathcal{D}\mid m,\theta)\) [from 【5】]，式子中是直接「給定」一組 \(\theta\) ，所以這個 \(\theta\) 怎麼來的、 \(\theta\) 出現的機率，這些都不在MLE的考量當中。

我們知道這樣並不好，假設以下有兩組 \(\theta\) 都可以得到一樣的Likelihood，依照你學機器學習和深度學習的經驗，你會喜歡哪組？

  • 第一組： \(\theta_1=0.5,\ \theta_2=0.1,\ \theta_3=-0.1\)
  • 第二組： \(\theta_1=1000.0,\ \theta_2=12.5,\ \theta_3=-500.0\)

以前的所學告訴我們第一組比較好，因為 \(\theta\) 接近 0，這樣的參數會讓我的輸入和輸出不會差異太大，Model會比較穩定，比較不會Overfitting，普遍作法是將Loss加入Regularization Term來壓低 \(\theta\) 的大小。

那麼這個Regularization Term究竟怎麼來的？

一開始學機器學習或深度學習時，你應該會覺得貿然的加上Regularization Term怪怪的，而今天你可以從這裡得到更好的解釋。神奇的是！當你在優化MAP時假設了參數 \(\theta\) 分布的同時，Regularization Term會被自然的推導出來，讓我們繼續看下去。

透過【3】式 \(p(\mathcal{D},m,\theta)\) 可以列出以下關係式：

$$ p(\mathcal{D}, m, \theta)=p(\mathcal{D},m\mid \theta)p(\theta)=p(\theta\mid \mathcal{D},m)p(\mathcal{D},m) \ \ ↪︎【18】 $$

稍作移項可得：

$$ p(\theta\mid \mathcal{D},m)=\frac{p(\mathcal{D},m\mid \theta)p(\theta)}{p(\mathcal{D},m)} \ \ ↪︎【19】 $$

因為 \(m\) 是給定的，我們想要將它向後移，使用【1】、【2】、【3】去轉換右式：

$$ \frac{p(\mathcal{D},m\mid \theta)p(\theta)}{p(\mathcal{D},m)}=\frac{p(\mathcal{D}\mid m,\theta)[p(m\mid \theta)p(\theta)]}{p(\mathcal{D\mid m})p(m)}＝\frac{p(\mathcal{D}\mid m,\theta)}{p(\mathcal{D}\mid m)}\frac{p(m,\theta)}{p(m)}=\frac{p(\mathcal{D}\mid m,\theta)p(\theta\mid m)}{p(\mathcal{D}\mid m)} \ \ ↪︎【20】 $$

於是我們得到了大名鼎鼎的貝氏定理： ⚠️

$$ p(\theta\mid \mathcal{D},m)=\frac{p(\mathcal{D}\mid m,\theta)p(\theta\mid m)}{p(\mathcal{D}\mid m)} \ \ ↪︎【21】 $$

其中：

  • \(p(\mathcal{D}\mid m,\theta)\) 就是Likelihood，Maximum這一項就是MLE，不用再特別討論。
  • \(p(\theta\mid m)\) 稱為先驗機率 (Prior Probability)，它所代表的意義正是描述 \(\theta\) 這個參數在給定 \(m\) 之後出現的機率有多大，這一項是先於經驗的，這裡的經驗指的是「這一次的實驗」，而這個 \(p(\theta\mid m)\) 是與本次實驗 \(\mathcal{D}\) 無關的。因此這個 \(p(\theta\mid m)\) 是需要人為給定的，你可以自己假設分布，例如：假設為有最少假設的Normal Distribution，或者是從過去的歷史紀錄去統計出 \(p(\theta\mid m)\) 也行。
  • \(p(\mathcal{D}\mid m)\) 稱為資料機率（probability of data），通常數據與模型的Hyperparameters應該是相互獨立的，所以其實可以簡寫成 \(p(\mathcal{D})\) ，這一項只需要統計一下Dataset的分布即可得到。
  • \(p(\theta\mid \mathcal{D},m)\) 稱為後驗機率 (Posterior Probability)，它所代表的意義是給定數據 \(\mathcal{D}\) 和 Hyperparameters \(m\) 之後，會出現 \(\theta\) 的機率，有注意到嗎？我們在【21】中同時連結了先驗機率和後驗機率，這代表的是手上原先有一個 \(\theta\) 分布（先驗機率），經過觀察數據後，我重新的去更新這個 \(\theta\) 分布（後驗機率），這充分的傳達了貝氏學派的演進概念。

後驗機率也是我們準備要最大化的目標，所以此方法才稱為Maximum A Posterior (MAP) 。

最大化後驗機率MAP是直接問貝氏定理什麼樣的 \(\theta\) 在給定條件下出現機率最大？而最大化Likelihood則是間接的希望找出一組 \(\theta\) 讓Model能產生Data的機率變高，兩者的優化邏輯是不一樣的。

從 【21】式出發：

$$ \theta_{MAP}=argmax_\theta\ p(\theta\mid \mathcal{D},m)=argmax_\theta\ \frac{p(\mathcal{D}\mid m,\theta)p(\theta\mid m)}{p(\mathcal{D}\mid m)} \ \ ↪︎【22】 $$

然後如【6】、【7】、【8】式一樣假設取樣是i.i.d. (independent and identically distributed)，得：

$$ \theta_{MAP}=argmax_\theta\ [\prod_{i}\ \frac{p(d_i\mid m,\theta)}{p(d_i\mid m)}]p(\theta\mid m) \ \ ↪︎【23】 $$

接下來，為了方便計算如【9】式取 \(\operatorname{ln}\)：

$$ \theta_{MAP}=argmax_\theta\ \{\sum_{i}\ [\operatorname{ln}p(d_i\mid m,\theta)-\operatorname{ln}p(d_i\mid m)]\}+\operatorname{ln}p(\theta\mid m) \ \ ↪︎【24】 $$

其中 \(-\operatorname{ln}p(d_i\mid m)\) 與 \(\theta\) 無關，可忽略：

$$ \theta_{MAP}=argmax_\theta\ \{\sum_{i}\ \operatorname{ln}p(d_i\mid m,\theta)\}+\operatorname{ln}p(\theta\mid m) \ \ ↪︎【25】 $$

第一項其實就是跟MLE一模模一樣樣，所以直接套用【9】到【14】式的推論，得：⚠️

$$ \theta_{MAP}=argmax_\theta\ \{\sum_{i}\ \operatorname{ln}p(y_i\mid x_i,m,\theta)\}+\operatorname{ln}p(\theta\mid m) \ \ ↪︎【26】 $$

觀察 【26】式，非常清楚的我們在優化第一項就如同優化MLE，但是MAP比MLE多了 \(\operatorname{ln}p(\theta\mid m)\) ，我們就針對這一項來討論，

  • 假設 \(p(\theta\mid m)\) 為一個Uniform Distribution，也就是說所有的 \(\theta\) 出現機率均等，則 \(p(\theta\mid m)=const.\)，這麼一來這一項在【26】式可以直接槓掉，因為它與 \(\theta\) 無關，此時 \(\theta_{MAP}=\theta_{MLE}\) 。所以說在貝氏學派的觀點下，MLE只是MAP的一個特例，MLE只是假設 \(\theta\) 出現機率均等的MAP，上一講有提過Uniform Distribution為所有分布當中Entropy最大的，也就是不確定程度最大的，也就是人為假設幾乎為零的分布，確實符合頻率學派的觀點：不需要太多人為假設。

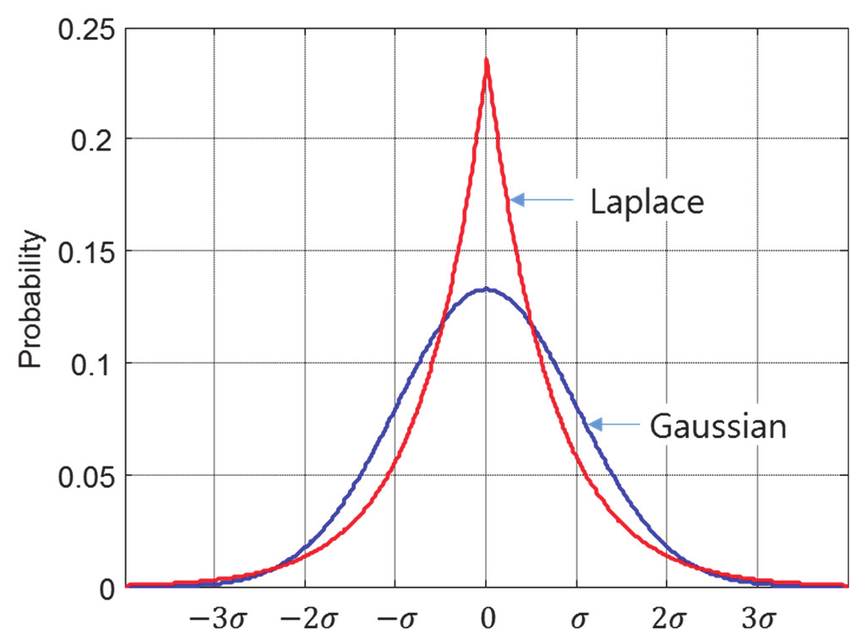
但是基於剛剛的推論 \(p(\theta\mid m)\) 的均等並不是我們想要的，我們希望 \(\theta\) 可以多出現在接近 \(\theta=0\) 的附近，因此我們希望 \(p(\theta\mid m)\) 的分布具有 有限Variance且平均值接近0 (\(E_{p(\theta\mid m)}[x]=0\))。此時的第一首選就是Normal Distribution，因為我們在第一講中說過：Normal Distribution是具有限Variance分布中具有最少人為假設的。

  • 假設 \(p(\theta\mid m)\) 為一個Normal Distribution且平均值為0，則
    $$ p(\theta\mid m)=\frac{1}{\sqrt{2\pi}\sigma}exp\{{-\frac{\theta^2}{2\sigma^2}}\} \ \ ↪︎【27】 $$
$$ \operatorname{ln}p(\theta\mid m)=\operatorname{ln}(\frac{1}{\sqrt{2\pi}\sigma})-\frac{\theta^2}{2\sigma^2} \ \ ↪︎【28】 $$

代入【26】，並且取負號，得

$$ \theta_{MAP}=argmin_\theta\ \sum_{i}-\operatorname{ln}p(y_i\mid x_i,m,\theta)+\frac{1}{2\sigma^2}\theta^2 \ \ ↪︎【29】 $$

哇！ L2 Regularization Term \(\frac{1}{2\sigma^2}\theta^2\) 就在這不經意間被導出了，所以未來看到L2 Regularization Term就要知道它隱藏了參數分布呈現Normal Distribution的假設。

可以預期的，當假設不同的參數分布 \(p(\theta\mid m)\) 就會得到不同型式的Regularization Term，如果我假設Laplace Distribution則會得到L1 Regularization Term，來看一下。

  • 假設 \(p(\theta\mid m)\) 為一個Laplace Distribution且平均值為0，則
    $$ p(\theta\mid m)=\frac{1}{2b}exp\{{-\frac{|\theta|}{b}}\} \ \ ↪︎【30】 $$
$$ \operatorname{ln}p(\theta\mid m)=\operatorname{ln}(\frac{1}{2b})-\frac{|\theta|}{b} \ \ ↪︎【31】 $$

代入【26】，並且取負號，得

$$ \theta_{MAP}=argmin_\theta\ \sum_{i}-\operatorname{ln}p(y_i\mid x_i,m,\theta)+\frac{1}{b}|\theta| \ \ ↪︎【32】 $$

第二項就是L1 Regularization Term。

Courtesy Youngjoo Kim

結語

這一講我們清楚的了解了頻率學派和貝氏學派各自的觀點，並且從兩者觀點出發去探討機器學習問題。

頻率學派使用Maximum Likelihood Estimation (MLE) 來優化，優化關係式如下：

$$ \theta_{MLE}=argmax_\theta\ \sum_{i}\ \operatorname{ln}p(y_i\mid x_i,m,\theta) $$

此項經過轉換會等同於最小化Data與Model之間的Cross Entropy，或等同於最小化Data與Model之間的KL Divergence，與上一講的資訊理論完美契合。

貝氏學派則使用Maximum A Posterior (MAP) 來優化，優化關係式如下：

$$ \theta_{MAP}=argmax_\theta\ \sum_{i}\ \operatorname{ln}p(y_i\mid x_i,m,\theta)+\operatorname{ln}p(\theta\mid m) $$

除了第一項與MLE一樣之外，此時我們還需考慮了參數可能的分布，當參數分布是均等時，MAP和MLE是等價的。但是我們希望 \(\theta\) 可以接近0，所以一般會去假設 \(p(\theta\mid m)\) 為一個Variance有限且平均值為0的分布，如果選擇使用Normal Distribution，則會得到L2 Regularization Term；如果選擇用Laplace Distribution，則會得到L1 Regularization Term。

本講已經給出了兩個觀點的機率優化式，但是要怎麼變換成擬合問題呢？這需要一大篇幅來介紹，我們會在下一講來仔細討論這個問題，敬請期待囉！

Reference

[此文章為原創文章，轉載前請註明文章來源]

Previous Post Next Post

Part 3 of the "剖析深度學習" series

Previous articles
Next articles