在上一次我們已經成功了安裝了IPython,這將會是我們這系列教學的主要舞台,而今天我要教大家在這個舞台上利用Numpy來做一些簡單的科學計算。
IPython
像上次一樣,打開IPython,緊接著把numpy和pandas載入,載入numpy之後我們習慣用as將它縮寫為np,pandas則縮寫為pd。
IPython是一個具有互動式介面的python執行介面,你可以一邊寫一邊理解目前的狀況,舉個例子
| >>> a = 12 # integer(整數)
>>> a # check variable a
12
|
在第一行中,我令變數a為12,而第二行只要把變數a直接key出來,我們就可以立刻查看變數裡頭有什麼內容,注意喔!在一般的python語言中,直接把變數key出來這件事是沒有意義的,這只有在IPython上才有的方便功能,有了這樣一個互動式的介面,讓我們在處理數據的時候可以隨時查看,目前數據的狀況。
Python常見的資料型別
Python常見的資料型別有整數(integer)、浮點數(floating-point number)、字串(string)、串列(list)、序對(tuple)、字典(dictionary),可以使用type()來查詢資料型別。
1
2
3
4
5
6
7
8
9
10
11
12 | >>> a = 10 # integer
>>> b = 40.0 # float, 必須有'.'
>>> c = 'word' # string
>>> d = [1, 2.0, '3'] # list
>>> e = (4, 5.0, '6') # tuple
>>> f = {'a':1, 'b':2 } # dictionary
>>> type(c)
str
>>> type(d)
list
>>> type(f)
dict
|
list和tuple裡面可以塞入任意的資料型別,甚至可以塞入另外一個list,或是自己定義的物件,list和tuple其實非常的相似,差異只在於tuple一旦決定了就不能在變更,但是list卻可以。
| >>> d.append('new')
>>> d
[1, 2.0, '3', 'new']
>>> d[0] = d[0] + 1 # 取出第一項(index=0)加一再設定回去第一項
>>> d
[2, 2.0, '3', 'new']
>>> del d[1] # 刪除index=1的那項
>>> d
[2, '3', 'new']
|
| >>> e.append('new') # fail
AttributeError: 'tuple' object has no attribute 'append'
>>> e[0]
4
>>> e[0] = e[0] + 1 # fail
TypeError: 'tuple' object does not support item assignment
>>> del e[1] # fail
TypeError: 'tuple' object doesn't support item deletion
|
在python中,整數和浮點數可以作簡單的四則運算
| >>> 1 + 2 * 2 - 6 / 2
2
>>> 1.0 + 2.0 * 2.0 - 6.0 / 2.0
2.0
>>> 3 ** 2 # 指數
9
|
一群整數做完運算輸出是整數,一群浮點數做完運算輸出是浮點數,那假如整數和浮點數混雜的情形呢?
| >>> 1 / 2
0 # 整數除整數,結果必定是整是,是整數0,而不是想像中的0.5,這種運算效果有點像求商
>>> 1 / 2.
0.5 # 只要有任意浮點數出現,整數強迫轉為浮點數,然後再做運算,這才是我們要的結果
>>> 3 ** 2.
9.0
|
所以在運算之前,你要想清楚你想要的目標是什麼?如果你有一個整數變數someInt接下來要作浮點數運算,可以使用float(someInt)強制先轉成浮點數再做接下來的運算,這樣比較不會犯錯。
事實上,轉成浮點數這樣的自動轉換在python中是很少見的,python是屬於強型別語言,所以型別和型別之間有很強的區份性,常常不會自動轉換,如果需要轉換必須要作額外的操作。
| >>> 1 + '2' # fail
TypeError: unsupported operand type(s) for +: 'int' and 'str'
>>> 1 + int('2') # 使用int()將字串轉成整數
3
|
常見的型別轉換函數有int(), float(), str(), list(), tuple()。所以如果要對一個tuple做更改,可以先轉成list再做運算。
| >>> f = (1,2,3)
>>> h = list(f)
>>> h
[1, 2, 3]
>>> h.insert(0,4) # 在index為0的地方插入整數4
>>> h
[4, 1, 2, 3]
|
Numpy的數學運算
在上一段我簡單介紹了python內建的運算,在大多數情況,內建的運算就已經足夠應付了,不過如果遇到複雜的運算,例如:三角函數、取最大最小值、exp、log、開根號、矩陣運算,我們就需要用到 Numpy 。
首先先介紹Numpy的一些數學運算,Numpy的數學運算詳細參考這。
我這邊舉幾個比較常見的例子。
1
2
3
4
5
6
7
8
9
10
11
12 | >>> np.sum([1,2,3]) # 加總
6
>>> np.max([1,2,3]) # 最大值
3
>>> np.min([1,2,3]) # 最小值
1
>>> np.mod(5,2) # 求餘數
1
>>> np.sin(np.pi/2.) # 求sin
1.0
>>> np.log(np.exp(1)) # ln 和 e
1.0
|
Numpy基礎元素:ndarray
Numpy最重要的元素就是ndarray,它是N-Dimensional Array的縮寫,在Numpy裡,dimesions被稱為axes,而axes的數量被稱為rank,axes是一個重要的概念,了解這個概念基本上就把Numpy搞懂一半以上了。
先來建立一個簡單1D的ndarray
| >>> A = np.array([1,2,3])
>>> A
array([1, 2, 3])
|
從外到內第一個遇到的中括號就是axis=0,往內就遞增上去,所以從1到2再到3,這個方向就叫做axis=0,Numpy大部分的運算都支援陣列的運算,經常你需要限制要在哪個axis方向上作運算,舉個例子
| >>> np.sum(A,axis=None) # axis為None的時候則加總所有元素
6
>>> np.sum(A,axis=0)
6
>>> np.sum(A,axis=1) # fail 因為A只有一維
ValueError: 'axis' entry is out of bounds
|
另外,也可以由內往外數,最內部的第一個中括後就是axis=-1,越外面就越負。
剛來上面的例子可能看不出效果,再來就稍微有趣一點,我們來看看2D的ndarray
| >>> B = np.array([[1,2,3],[4,5,6]])
>>> B
array([[1, 2, 3],
[4, 5, 6]])
>>> np.sum(B,axis=0)
array([5, 7, 9]) # [1+4, 2+5, 3+6]
>>> np.sum(B,axis=1)
array([ 6, 15]) # [1+2+3, 4+5+6]
|
有看懂axis怎麼運作嗎?最外面的中括號是axis=0,它包含[1,2,3]和[4,5,6]兩個元素,方向就是從[1,2,3]到[4,5,6]的方向,在這個方向上做sum,所以結果就會得到[1+4, 2+5, 3+6]。若是axis=1則是第二層中括號,也就是1到3和4到5的方向,所以結果會是[1+2+3, 4+5+6]。
一樣從內而外也可以,如果axis=None或defalut情形下,則是對矩陣內所有元素作運算。
| >>> np.sum(B)
21
>>> np.sum(B, axis=None) # same as above
21
>>> np.sum(B, axis=-1) # 和axis=1等價
array([ 6, 15])
|
相信大家已經有感覺了,那3D也是一樣道理的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | >>> C = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
>>> C
array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]])
>>> np.sum(C,axis=0)
array([[ 8, 10, 12], # [1+7, 2+8, 3+9 ]
[14, 16, 18]]) # [4+10, 5+11, 6+12]
>>> np.sum(C,axis=1)
array([[ 5, 7, 9], # [1+4, 2+5, 3+6]
[17, 19, 21]]) # [7+10, 8+11, 9+12]
>>> np.sum(C,axis=2)
array([[ 6, 15], # [1+2+3, 4+5+6]
[24, 33]]) # [7+8+9, 10+11+12]
|
畫張圖可能比較好理解一點,在各個方向上加總的結果都不一樣。
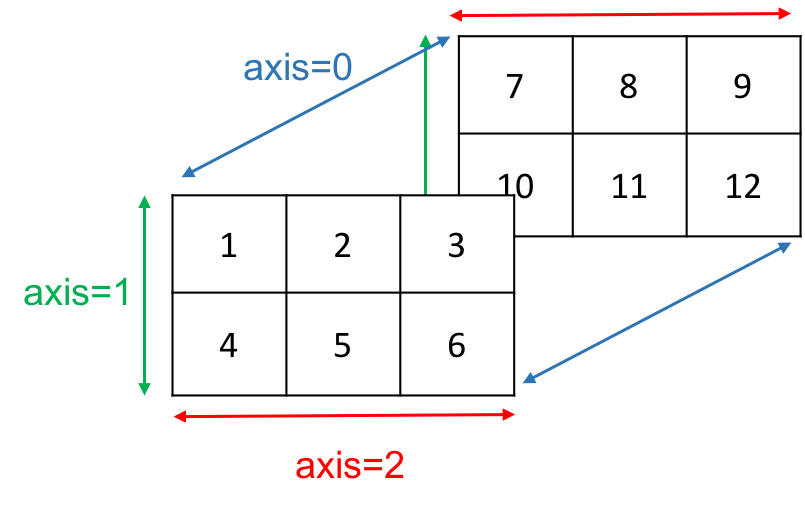
同樣,axis的概念也可以用在矩陣的shape
| >>> D = np.array([[1,2],[3,4],[5,6]])
>>> D
array([[1, 2],
[3, 4],
[5, 6]])
>>> D.shape
(3, 2)
|
(3, 2)這樣的shape我們就一點都不意外了,axis=0有三個元素,而axis=1有兩個元素。shape可以直接改,如果數量恰當的話就會自動重組。
| >>> D.shape = (2,1,3)
>>> D
array([[[1, 2, 3]],
[[4, 5, 6]]])
|
axis=0有兩個元素,axis=1有一個元素,axis=2有三個元素。
同樣的概念也可以用在取出單一元素上。
| >>> D[1, 0, 1]
5
>>> D[0, 0, 2]
3
|
在axis=0上選第二個元素(1),在axis=1上選第一個元素(0),在axis=2上選第二個元素(1),所以選出來的元素就是5啦!
有了axis的概念,我們來看另外一個重要的概念—dtype。
ndarray有其資料型別,這個資料型別就稱為dtype,有哪些內建的資料型別呢?我們可以透過numpy的內建資料來查看。
| >>> np.sctypes
{'complex': [numpy.complex64, numpy.complex128, numpy.complex256],
'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128],
'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64],
'others': [bool, object, str, unicode, numpy.void],
'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64]}
|
有複數、浮點數、整數,另外每個資料型別還可以由資料的儲存容量大小來區分,例如:numpy.int32就代表是容量為32bits的整數。我們可以在設置ndarray的時候事先強迫設成某資料型別。
| >>> t1 = np.array([1,2,3],dtype='int32')
>>> t1
array([1, 2, 3], dtype=int32)
>>> t1.dtype
dtype('int32')
>>> t2 = np.array([1,2,3],dtype='float64')
>>> t2
array([ 1., 2., 3.])
>>> t2.dtype
dtype('float64')
|
Numpy的矩陣運算
有了ndarray就可以作矩陣的運算了,矩陣運算有兩種系統,一種是element-wise(元素方面) operation,一種是matrix operation。
這樣講好像很抽象,我來解釋一下,element-wise operation就是每個元素獨立運算,例如,以下例子就是element-wise的相加。
| >>> A = np.array([[1,2],[3,4]],dtype='float64')
>>> B = np.array([[5,0],[0,0]],dtype='float64')
>>> A+B # element-wise plus
array([[ 6., 2.],
[ 3., 4.]])
|
A和B矩陣中同樣位置的元素相加,再放到新的矩陣中,這一種操作就叫做element-wise operation。
在numpy中如果沒有特別指定,所有的運算都是這類的運算,我們來看一下減、乘和除。
| >>> A-B # element-wise minus
array([[-4., 2.],
[ 3., 4.]])
>>> A*B # element-wise multiply
array([[ 5., 0.],
[ 0., 0.]])
>>> B/A # element-wise divide
array([[ 5., 0.],
[ 0., 0.]])
|
那我如果想要作矩陣操作(matrix operation)呢?譬如說矩陣內積,
| >>> np.dot(A,B) # 矩陣內積
array([[ 5., 0.],
[ 15., 0.]])
|
還有更多的矩陣操作,
矩陣轉置
| >>> A = np.array([[1,2],[3,4]],dtype='float64')
>>> A
array([[ 1., 2.],
[ 3., 4.]])
>>> A.T # 矩陣轉置
array([[ 1., 3.],
[ 2., 4.]])
|
反矩陣
| >>> A_rev = np.linalg.inv(A) # 反矩陣
>>> A_rev
array([[-2. , 1. ],
[ 1.5, -0.5]])
>>> np.dot(A,A_rev)
array([[ 1.00000000e+00, 0.00000000e+00],
[ 8.88178420e-16, 1.00000000e+00]])
|
A和A的反矩陣內積為單位矩陣,你有注意到8.88178420e-16這個奇怪的數字嗎?這是因為python在計算的過程有一些誤差的緣故,所以才會產生一個這麼小的數字,但基本上可以看作是0。
另外矩陣跟矩陣間也可以合併。
垂直方向合併
| >>> A = np.array([[1,2],[3,4]],dtype='float64')
>>> B = np.array([[5,0],[0,0]],dtype='float64')
>>> V = np.vstack((A,B))
>>> V
array([[ 1., 2.],
[ 3., 4.],
[ 5., 0.],
[ 0., 0.]])
|
水平方向合併
| >>> H = np.hstack((A,B))
>>> H
array([[ 1., 2., 5., 0.],
[ 3., 4., 0., 0.]])
|
當然也可以分割矩陣,
垂直方向分割
| >>> np.vsplit(V,2) # 2代表切兩份
[array([[ 1., 2.],
[ 3., 4.]]), array([[ 5., 0.],
[ 0., 0.]])]
|
水平方向分割
| >>> np.hsplit(H,4) # 4代表切四份
[array([[ 1.],
[ 3.]]), array([[ 2.],
[ 4.]]), array([[ 5.],
[ 0.]]), array([[ 0.],
[ 0.]])]
|
子彈總結
- Python常見的資料型別:整數(integer)、浮點數(floating-point number)、字串(string)、串列(list)、序對(tuple)、字典(dictionary)
- ndarray的axes概念很重要,這會決定函數操作的方式,例如:np.sum
- ndarray的資料型別(dtype),例如:'float64', 'int64', 'string', ...
- numpy的矩陣運算有element-wise operation和matrix operation兩種
Numpy的基礎概念我們已經有了,在下一篇當中會再更深入的了解Numpy還有什麼進階的功能,包括:產生ndarray的多種方法、broadcast的概念以及ndarray的進階操作手法。

